Can a Trie be implemented efficiently?

Question

What is the most space and time efficient way to implement a Trie in Mathematica?

Will it be practically faster than what is natively available in appropriate cases?

Answer 1

UPDATE

Since version 10, we have Associations. Here is the modified code for trie building and querying, based on Associations. It is almost the same as the old code (which is below):

ClearAll[makeTreeAssoc];
makeTreeAssoc[wrds : {__String}] := Association@makeTreeAssoc[Characters[wrds]];
makeTreeAssoc[wrds_ /; MemberQ[wrds, {}]] := 
    Prepend[makeTreeAssoc[DeleteCases[wrds, {}]], {} -> {}];
makeTreeAssoc[wrds_] := 
   Reap[
     If[# =!= {}, Sow[Rest[#], First@#]] & /@ wrds, 
     _, 
     #1 -> Association@makeTreeAssoc[#2] &
   ][[2]]

You can see that the only difference is that Association is added to a couple of places, otherwise it's the same code. The lookup functions also are very similar:

ClearAll[getSubTreeAssoc];
getSubTreeAssoc[word_String, tree_] := Fold[Compose, tree, Characters[word]]

ClearAll[inTreeQAssoc];
inTreeQAssoc[word_String, tree_] := KeyExistsQ[getSubTreeAssoc[word, tree], {}]

The tests similar to the ones below (for entire dictionary) show that the lookup based on this trie (Associations - based) is about 3 times faster than the one based on rules, for a trie built from a dictionary. The new implementation of getWords is left as an exercise to the reader (in fact, that function could be optimized a lot, by storing entire words as leaves in the tree, so that one doesn't have to use StringJoin and combine the words).

---

A combination of rules and recursion is able to produce rather powerful solutions. Here is my take on it:

ClearAll[makeTree];
makeTree[wrds : {__String}] := makeTree[Characters[wrds]];
makeTree[wrds_ /; MemberQ[wrds, {}]] := 
     Prepend[makeTree[DeleteCases[wrds, {}]], {} -> {}];
makeTree[wrds_] := 
    Reap[If[# =!= {}, Sow[Rest[#], First@#]] & /@ 
       wrds, _, #1 -> makeTree[#2] &][[2]]

ClearAll[getSubTree];
getSubTree[word_String, tree_] := Fold[#2 /. #1 &, tree, Characters[word]]

ClearAll[inTreeQ];
inTreeQ[word_String, tree_] :=  MemberQ[getSubTree[word, tree], {} -> {}]

ClearAll[getWords];
getWords[start_String, tree_] :=
  Module[{wordStack = {}, charStack = {}, words},
    words[{} -> {}] :=
      wordStack = {wordStack, StringJoin[charStack]};
    words[sl_ -> ll_List] :=
      Module[{},
        charStack = {charStack, sl};
        words /@ ll;
        charStack = First@charStack;
      ];
    words[First@Fold[{#2 -> #1} &, getSubTree[start, tree], 
         Reverse@Characters[start]]
    ];
    ClearAll[words];
    Flatten@wordStack];

The last function serves to collect the words from a tree, by performing a depth-first tree traversal and maintaining the stack of accumulated characters and words.

Here is a short example:

In[40]:= words = DictionaryLookup["absc*"]
Out[40]= {abscess,abscessed,abscesses,abscessing,abscissa,abscissae,abscissas,
   abscission,abscond,absconded,absconder,absconders,absconding,absconds}

In[41]:= tree = makeTree[words]
Out[41]= {a->{b->{s->{c->{e->{s->{s->{{}->{},e->{d->{{}->{}},s->{{}->{}}},
      i->{n->{g->{{}->{}}}}}}},i->{s->{s->{a->{{}->{},e->{{}->{}},s->{{}->{}}},
        i->{o->{n->{{}->{}}}}}}},o->{n->{d->{{}->{},e->{d->{{}->{}},r->{{}->{},s->{{}->{}}}},
       i->{n->{g->{{}->{}}}},s->{{}->{}}}}}}}}}}

In[47]:= inTreeQ[#,tree]&/@words
Out[47]= {True,True,True,True,True,True,True,True,True,True,True,True,True,True}

In[48]:= inTreeQ["absd",tree] 
Out[48]= False

In[124]:= getWords["absce", tree]
Out[124]= {"abscess", "abscessed", "abscesses", "abscessing"}

I only constructed here a bare-bones tree, so you can only test whether or not the word is there, but not keep any other info. Here is a larger example:

In[125]:= allWords =  DictionaryLookup["*"];

In[126]:= (allTree = makeTree[allWords]);//Timing
Out[126]= {5.375,Null}

In[127]:= And@@Map[inTreeQ[#,allTree]&,allWords]//Timing
Out[127]= {1.735,True}

In[128]:= getWords["pro",allTree]//Short//Timing
Out[128]= {0.015,{pro,proactive,proactively,probabilist,
    <<741>>,proximate,proximately,proximity,proxy}}

In[129]:= DictionaryLookup["pro*"]//Short//Timing
Out[129]= {0.032,{pro,proactive,proactively,probabilist,<<741>>,
    proximate,proximately,proximity,proxy}}

I don't know which approach has been used for the built-in functionality, but the above implementation seems to be generally in the same calss for performance. The slowest part is due to the top-level tree-traversing code in getWords. It is slow because the top-level code is slow. One could speed it up considerably by hashing words to integers - then it can be Compiled. This is how I'd do that, if I were really concerned with speed.

EDIT

For a really nice application of a Trie data structure, where it allows us to achieve major speed-up (w.r.t. using DictionaryLookup, for example), see this post, where it was used it to implement an efficient Boggle solver.

Answer 2

This might not give you the answer you expect, neither is this better than Leonid's solution, but. Since your fairly general question leaves a lot of room for answers and since I felt that it might be relevant, I gave it a go.

Assuming, that we have a list of prefix representations of a string (e.g. from here), it can be plotted easily with TreeForm:

decompTree = {"ar", {"c", {"h", {{"b", {"i", {"s", {{"h", {"o", {"p"}}},
      {"ho", {"p"}}}}}}, {"bi", {"s", {{"h", {"o", {"p"}}}, {"ho", {"p"}}}}}}}}};
TreeForm[decompTree, VertexRenderingFunction -> (Style[Text[#2, #1], 14, 
     Background -> White] &), ImageSize -> 400]

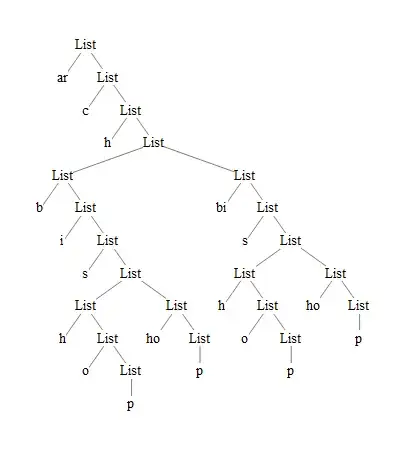
Now let's convert it to a graph. First, assign a unique integer to each leaf:

decompList = Cases[decompTree //. {x__String, y__List} :>
    (Join[{x}, #] & /@ {y}), {__String}, \[Infinity]];
vertexRep = Thread[Range@Length@# -> #] &@ Cases[decompTree, _String, \[Infinity]];
counter = 1;
vertexTree = Replace[decompTree, _String :> counter++, \[Infinity]]

{1, {2, {3, {{4, {5, {6, {{7, {8, {9}}}, {10, {11}}}}}}, {12, {13, 
    {{14, {15, {16}}}, {17, {18}}}}}}}}}

And then building the edge list of the graph by traversing all possible routes with ReplaceRepeated in the (now integer-valued) decomposition tree:

edgeTree = vertexTree //. {{x_Integer, {y_Integer, z___}} :> {x -> y, {y, z}},
    {x_Integer, y : {__List}} :> {x -> First@# & /@ y, y}};
edgeList = Cases[edgeTree, _Rule, \[Infinity]];
TreePlot[edgeList, Left, VertexRenderingFunction -> (Style[Text[#2 /. vertexRep, #1], 14, 
     Background -> White] &), ImageSize -> 400]

Answer 3

The Markdown document

• "Tries with frequencies in Java"

(and this blog post) describe the installation and use in Mathematica of Tries with frequencies implemented in Java through a corresponding Mathematica package. Note that the set-up requires some efforts.

Basic examples

Basic examples can be found in this album of images that shows the "JavaTrie.*" commands with their effects:

More detailed explanations can be found in the Markdown document.

Performance evaluation (finding dictionary infixes)

The following performance tests are done on a 2015 MacBook Pro. The query timings are almost the same as those of Leonid's implementation; the creation timings are 5-10 times smaller.

Get all words from a dictionary (~93,000):

allWords =  DictionaryLookup["*"];
allWords // Length

(* 92518 *)

Trie creation and shrinking:

AbsoluteTiming[
 jDTrie = JavaTrieCreateBySplit[allWords];
 jDShTrie = JavaTrieShrink[jDTrie];
]

(* {0.30508, Null} *)

JSON form extraction:

AbsoluteTiming[
 jsonRes = JavaTrieToJSON[jDShTrie];
]

(* {3.85955, Null} *)

(The data transfer from Java to Mathematica takes time...)

Here are the node statistics of the original and shrunk tries:

JavaTrieNodeCounts[jDTrie]
(* <|"total" -> 224937, "internal" -> 160090, "leaves" -> 64847|> *)

JavaTrieNodeCounts[jDShTrie]
(* <|"total" -> 115504, "internal" -> 50657, "leaves" -> 64847|> *)

Find the infixes that have more than three characters and appear more than 10 times:

Multicolumn[#, 4] &@
 Select[SortBy[
   Tally[Cases[
     jsonRes, ("key" -> v_) :> v, Infinity]], -#[[-1]] &], StringLength[#[[1]]] > 3 && #[[2]] > 10 &]