Add coordinate axes to a 3D plot of concentric spheres

Question

I want to add coordinate axis to a figure of nested spheres.

I have the command.

Graphics3D[Table[{Opacity[.6], Specularity[White, 20], Sphere[{0, 0, 0}, r]}, 
{r, 1/2, 3, 1/2}], Boxed -> False]

Which reproduces the set of nested spheres

Now, I would need to add axes X, Y and Z

It would also be good to be able to label the spheres 1, 2, 3...

Thanks Edit: and to do something similar to this picture?

Answer 1

options = {Mesh -> None, Boxed -> False, Axes -> True,  AxesOrigin -> {0, 0, 0}, 
   PlotStyle -> Directive[Opacity[.6], Specularity[White, 20]], ImageSize -> 500};
SphericalPlot3D[{1, 2, 3}, {t, 0, Pi}, {p , 0, 3 Pi/2},  Evaluate@options]

or

ParametricPlot3D[{Cos[u] Sin[v], Sin[u] Sin[v], Cos[v]} # & /@ {1, 2, 3}, 
  {v, 0, Pi}, {u, 0, 2 Pi}, 
  Evaluate@options, RegionFunction -> Function[{x, y}, x y > 0 || y > 0]]

or

ContourPlot3D[x^2 + y^2 + z^2, {x, -2, 2}, {y, -2, 2}, {z, -2, 2}, 
   Contours -> {1, 2, 3}, Evaluate[options /. PlotStyle -> ContourStyle],
   BoundaryStyle -> None, RegionFunction -> Function[{x, y}, x y > 0 || y > 0]]

or

Show[RevolutionPlot3D[{# Cos[t], # Sin[t]}, {t, -Pi/2, Pi/2}, {v, Pi/2, 2 Pi},
     Evaluate@options] & /@ {3, 2, 1}]

Answer 2

From the documentation of SphericalPlot3D you can find:

SphericalPlot3D[{1, 2, 3}, {θ, 0, Pi}, {ϕ, 0, 3 Pi/2}]

Thus, you can modify it a little:

r = {1, 2, 3};
col = Hue@.5;
opts = {Mesh -> None, Boxed -> False, Axes -> False};
spheres = SphericalPlot3D[Evaluate@r, {\[Theta], 0, Pi}, {\[Phi], 0, 3 Pi/2}, 
  Evaluate@opts, PlotStyle -> (Directive[Opacity@(1/#), col] & /@ r)];
(*axes and labels*)
al = Graphics3D[{Style[Text[#, RotateLeft@#2], Bold, 15] & @@@ 
  Thread[{{"X", "Y", "Z"}, RotateRight[{Max@r + Max@r/10, 0, 0}, #] & /@ {0, 1, 2}}], 
  Inset[Style[#, Bold, 20], {(Sqrt@2)/2 #, 0, (Sqrt@2)/2 #}] & /@ r}, 
  PlotRange -> Max@r, Boxed -> False, Axes -> True, AxesOrigin -> {0, 0, 0}];
filling[{rmin_, rmax_}] := ParametricPlot3D[{r*{0, -1 Sin[t], Cos[t]}, 
  r*{Sin[t], 0, Cos[t]}}, {r, rmin, rmax}, {t, 0, Pi}, 
  Evaluate@opts, PlotStyle -> (Directive[EdgeForm[], Opacity@.75, col])];
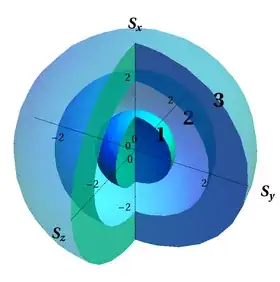
Show[{al, spheres, filling[{0, Min@r}], filling[r[[2 ;; 3]]]}]

---

Edit:

It's now easier to chose where to place the axes labels:

r = {1, 2, 3};
col = Hue@.5;
opts = {Mesh -> None, Boxed -> False, Axes -> False};
spheres = SphericalPlot3D[Evaluate@r, {\[Theta], 0, Pi}, {\[Phi], 0, 3 Pi/2}, 
  Evaluate@opts, PlotStyle -> (Directive[Opacity@(1/#), col] & /@ r)];
(*axes and labels*)
al = Graphics3D[{Style[Text[#, RotateLeft@#2], Bold, 15] & @@@ 
  {{Subscript[S, x], {Max@r + .5, 0, 0}}, 
   {Subscript[S, x], {0, Max@r + .5, 0}}, 
   {Subscript[S, x], {0, 0, -Max@r - .5}}}, 

  Inset[Style[#, Bold, 20], {(Sqrt@2)/2 #, 0, (Sqrt@2)/2 #}] & /@ r}, 
  PlotRange -> Max@r, Boxed -> False, Axes -> True, AxesOrigin -> {0, 0, 0}];
filling[{rmin_, rmax_}] := ParametricPlot3D[{r*{0, -1 Sin[t], Cos[t]}, 
  r*{Sin[t], 0, Cos[t]}}, {r, rmin, rmax}, {t, 0, Pi}, 
  Evaluate@opts, PlotStyle -> (Directive[EdgeForm[], Opacity@.75, col])];
Show[{al, spheres, filling[{0, Min@r}], filling[r[[2 ;; 3]]]}]