Toady I want to build geometry as shown below:

I know the Mathematica owns the built-in like Cylinder[], Sphere[] and so on, but it lacks of a function that could construct user-defined geometry, so I have a trial as below:
TengentLine
lineCofficient[x1_, y1_, r1_, x2_, y2_, r2_, style_] := Block[
{},
First@Solve[
{(k x1 - y1 + b)/Sqrt[1 + k^2] == r1 style,
(k x2 - y2 + b)/Sqrt[1 + k^2] == r2 style},
{k, b}]
]
tangentPoint
tangentPoint[x1_, y1_, r1_, x2_, y2_, r2_, style_] := Block[
{k, b},
{
Solve[
{y == k x + b /.lineCofficient[x1, y1, r1, x2, y2, r2,style],
(x - x1)^2 + (y - y1)^2 == r1^2}, {x, y}],
Solve
[{y == k x + b /. lineCofficient[x1, y1, r1, x2, y2,r2,style],
(x - x2)^2 + (y - y2)^2 == r2^2}, {x, y}]
} // Flatten[#, 1] &
]
My geometry
FinalGeometry[x1_, y1_, z1_, r1_, x2_, y2_, z2_, r2_, h_] := Block[
{x, y, one, two, three, four},
Graphics3D[
{Cylinder[{{x1, y1, z1}, {x1, y1, h}}, r1],
Cylinder[{{x2, y2, z2}, {x2, y2, h}}, r2],
one = Flatten[
List[
Join[{x, y} /.tangentPoint[x1, y1, r1, x2, y2, r2, -1], {{z1}, {z1}}, 2],
Join[{x, y} /.tangentPoint[x1, y1, r1, x2, y2, r2, -1], {{h}, {h}}, 2]], 1];
two = Flatten[
List[
Join[{x, y} /.tangentPoint[x1, y1, r1, x2, y2, r2, 1], {{z1}, {z1}}, 2],
Join[{x, y} /. tangentPoint[x1, y1, r1, x2, y2, r2, 1], {{h}, {h}}, 2]], 1];
three = Flatten[
List[
Join[{x, y} /.tangentPoint[x1, y1, r1, x2, y2, r2, -1], {{z1}, {z1}}, 2],
Join[{x, y} /.tangentPoint[x1, y1, r1, x2, y2, r2, 1], {{z1}, {z1}}, 2]], 1];
four = Flatten[
List[
Join[{x, y} /.tangentPoint[x1, y1, r1, x2, y2, r2, -1], {{h}, {h}}, 2],
Join[{x, y} /.tangentPoint[x1, y1, r1, x2, y2, r2, 1], {{h}, {h}}, 2]], 1];
Sequence @@
(Polygon /@
Flatten[{Partition[one, 3, 1], Partition[two, 3, 1],
Partition[three, 3, 1], Partition[four, 3, 1]}, 1])
},
BoxRatios -> Automatic
]
]
Using my function:
FinalGeometry[0, 0, 0, 3, 12, 0, 0, 2, 2]
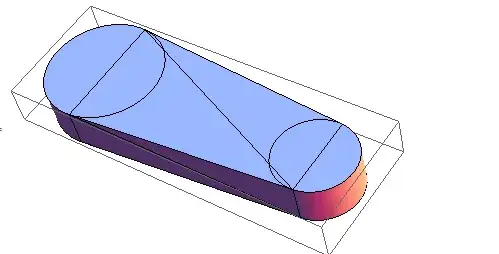
However, I felt my method is tedious and ingeneral. In addition, there are many other geometry "by extruding a section" like 3D software Autodesk Inventor.
So my question is:
Is there a good and easy method to realize my function
FinalGeometry[]?Is there possible to construct a function that can generate a geometry that can rotate freely (not a static image) by extruding a section?
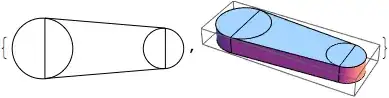
isn't duplicte,because (6206) isjust a image,not a geomatry that can rotate. – xyz Jul 21 '14 at 12:58ColorReplace and Raster3Dis not in V8,in addition,halirutan's solution takes many time to calculate and it is hard to rotate. – xyz Jul 21 '14 at 14:39extrude = {0, 0, 1}; rule2Dto3D = {x_?AtomQ, y_?AtomQ} :> {x, y, 0}; ruleLine2Polygon = Line[{p_?VectorQ, q_?VectorQ}] :> Polygon[{p, q, q + extrude, p + extrude}]; ruleCircle2Cylinder = Circle[p_?VectorQ, r_?AtomQ] :> Cylinder[{p, p + extrude}, r]; object2D = {Line[{{0, 0}, {8, 0}}], Circle[{0, 0}, 2], Circle[{8, 0}, 1]}; object3D = object2D /. rule2Dto3D /. {ruleLine2Polygon, ruleCircle2Cylinder}; {Graphics@object2D, Graphics3D@object3D}. It is limited to extruding line segments and circles, but extra 2D to 3D rules could be added. – Stephen Luttrell Jul 21 '14 at 14:53