Here is extensions to @Jens answer (I think) also relying on possible separation of variable. It is not meant as an independent answer, but complements it.
First extend his answer to 2D
ClearAll[pt, px, x, t, p];
operator = Function[p, D[p, t] - Δ D[p, x, x] - Δ D[p, y, y]];
ansatz = pt[t] px[x] py[y];
pde2 = Expand[Apply[Subtract, operator[ansatz]/ansatz == 0]];
ptSolution = First@DSolve[Select[pde2, (D[#, x] == 0 &&
D[#, y] == 0) &] == κ1^2 + κ2^2, pt[t], t];
pxSolution = First@DSolve[Select[pde2, D[#, x] =!= 0 &] == -κ1^2, px[x],
x, GeneratedParameters -> b1];
pySolution = First@DSolve[Select[pde2, D[#, y] =!= 0 &] == -κ2^2, py[y],
y, GeneratedParameters -> b2];
sol = ansatz /. Join[ptSolution, pxSolution, pySolution]
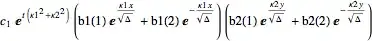
I can then integrate over the constants
sol1 = Integrate[(sol /. κ1 -> I κ1), {κ1, -Infinity, Infinity}];
sol2 = Integrate[(sol1 /. κ2 -> I κ2), {κ2, -Infinity, Infinity}]

And check that this solution works
operator[sol2] // Simplify
See also this and that solution by @Jens via separation of variable
Try Anisotropic diffusion
Clear[operator];operator[p_] := D[p, t] - Δx D[p, x, x] - Δy D[p, y, y]
ansatz = pt[t] px[x] py[y]; operator[p[t, x, y]]
(*
==> ∂p/∂t - Δx ∂^2p/∂x^2 - Δy ∂^2p/∂y^2
*)
pde2 = Expand[Apply[Subtract, operator[ansatz]/ansatz == 0]];
ptSolution = First@DSolve[Select[pde2, (D[#, x] == 0 &&D[#, y] == 0) &] ==
κ1^2 + κ2^2, pt[t], t];
pxSolution =First@DSolve[Select[pde2, D[#, x] =!= 0 &] == -κ1^2, px[x],
x, GeneratedParameters -> a];
pySolution = First@DSolve[Select[pde2, D[#, y] =!= 0 &] == -κ2^2, py[y],
y, GeneratedParameters -> b];
sol = ansatz /. Join[ptSolution, pxSolution, pySolution]
sol1 = Integrate[(sol /. κ1 -> I κ1), {κ1, -Infinity, Infinity}];
sol2 = Integrate[(sol1 /. κ2 ->I κ2), {κ2, -Infinity, Infinity}];

UPDATE
We can move to a generic coordinate system;
Let's define the Laplacian
Clear[lap];
lap[p_, coord_: "Cartesian"] :=
Laplacian[p, {x, y, z}, coord] // Expand
Let us first try and solve in Cylindrical coordinates
Clear[operator];operator[p_] := D[p, t] - Δ lap[p, "Cylindrical"]
Format[a[i_]] = Subscript[a, i]; Format[b[i_]] = Subscript[b, i];
We chose an ansatz which is mute in y (=theta) (making assumptions about the boundary
condition)
ansatz = pt[t] px[x] pz[z];
pde2 = Expand[Apply[Subtract, operator[ansatz]/ansatz == 0]];
ptSolution =
First@DSolve[Select[pde2, (D[#, x] == 0 && D[#, y] == 0 &&
D[#, z] == 0) &] == κ1^2 + κ3^2, pt[t], t];
pxSolution =
First@DSolve[Select[pde2, D[#, x] =!= 0 &] == -κ1^2, px[x], x,
GeneratedParameters -> a];
pzSolution =
First@DSolve[Select[pde2, D[#, z] =!= 0 &] == -κ3^2, pz[z],
z, GeneratedParameters -> b];
sol = ansatz /. Join[ptSolution, pxSolution, pzSolution]
sol1 = Integrate[(sol /. κ1 -> I κ1), {κ1, 0, Infinity}];
sol2 = Integrate[(sol1 /. κ3 -> I κ3), {κ3, -Infinity, Infinity}]

operator[sol2] /. z -> 2 /. x -> 1 /. t -> 2 /. Δ -> 1 //N // Expand // Chop
(* 0 *)
Let's now try in spherical coordinates
Clear[operator]; operator[p_] := D[p, t] - Δ lap[p, "Spherical"]
We chose an ansatz which is mute in y,z (=theta,phi)
ansatz = pt[t] px[x] ;
pde2 = Expand[Apply[Subtract, operator[ansatz]/ansatz == 0]]
ptSolution = First@DSolve[Select[pde2, (D[#, x] == 0 && D[#, y] == 0 &&
D[#, z] == 0) &] == κ1^2, pt[t], t];
pxSolution = First@DSolve[Select[pde2, D[#, x] =!= 0 &] == -κ1^2, px[x], x,
GeneratedParameters -> a];
sol1 = Integrate[(sol /. κ1 -> I κ1), {κ1, 0, Infinity}] // Simplify
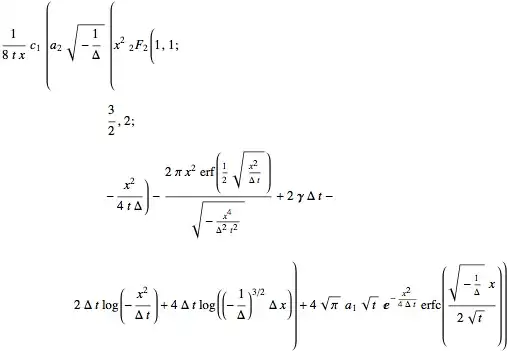
Check that this solution is ok
operator[sol1] /. x -> 1 /. t -> 2 /. Δ -> 1 // N // Expand // Chop
(* ==> 0 *)
Note that this works also in 2D for, e.g. Polar coordinates
Clear[operator];operator[p_] := D[p, t] - Δ Laplacian[p, {x, y}, "Polar"];
ansatz = pt[t] px[x] ;
pde2 = Expand[Apply[Subtract, operator[ansatz]/ansatz == 0]];
ptSolution = First@DSolve[Select[pde2, (D[#, x] == 0 && D[#, y] == 0 &&
D[#, z] == 0) &] == κ1^2, pt[t], t];
pxSolution =First@DSolve[Select[pde2, D[#, x] =!= 0 &] == -κ1^2, px[x], x,
GeneratedParameters -> a];
sol = ansatz /. Join[ptSolution, pxSolution];
sol1 = Integrate[(sol /. κ1 -> I κ1), {κ1, 0,Infinity}] // Simplify

operator[sol1] //FullSimplify
(* ==> 0 *)
UPDATE 2
We can move to a more general class of heat equations:
Clear[operator];
operator[p_] := D[p, t] - x Δ D[p, {x, 2}]
Note the extra x in front of Δ
ansatz = pt[t] px[x] ;
pde2 = Expand[Apply[Subtract, operator[ansatz]/ansatz == 0]]
(*
==> d pt/dt/pt(t) - (Δ x d^2px/dx^2)/ px(x)
*)
ptSolution = First@DSolve[Select[pde2, (D[#, x] == 0 && D[#, y] == 0 &&
D[#, z] == 0) &] == κ^2, pt[t], t];
pxSolution = First@DSolve[Select[pde2, D[#, x] =!= 0 &] == -κ^2, px[x], x,
GeneratedParameters -> a];
sol = ansatz /. Join[ptSolution, pxSolution];
sol1 = Integrate[(sol /. κ -> I κ), {κ, 0, Infinity}]

operator[sol1] //FullSimplify
(* ==> 0 *)
Following exactly the same steps,
operator[p_] := D[p, t] - Δ D[1/x D[p, x], x]
yields for instance:

which I think, demonstrates the potential versatility of mathematica in this context.
This can be encapsulated as a prototype of what DSolve could eventually do
as follows:
Clear[Heat];
Heat[factor_: Δ, b1_: - Infinity, b2_: Infinity] :=
Module[{operator, pde2, ansatz, ptSolution, pxSolution, sol, sol1,pt, px, κ},
operator[p_] := D[p, t] - D[factor D[p, x], x];
Print[{operator[f[t, x]] == 0, b1, b2} // TableForm];
ansatz = pt[t] px[x] ;
pde2 = Expand[Apply[Subtract, operator[ansatz]/ansatz == 0]];
ptSolution = First@DSolve[Select[pde2, (D[#, x] == 0 && D[#, y] == 0 &&
D[#, z] == 0) &] == κ^2, pt[t], t];
pxSolution = First@DSolve[Select[pde2, D[#, x] =!= 0 &] == -κ^2, px[x],
x, GeneratedParameters -> a];
sol = ansatz /. Join[ptSolution, pxSolution];
sol1 = Integrate[(sol /. κ -> I κ), {κ, b1,b2},Assumptions->t>0];
operator[sol1] /. Δ -> 1 /. x -> 2 /. t -> 3 // N //
Expand // Chop // If[# != 0, Print["not ok!"]] &; sol1];
so that, e.g.
Heat[Δ, -Infinity]
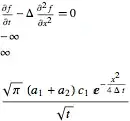
Heat[Δ x, 0]
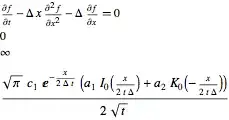
Heat[x^n, 0]

sol1 = Heat[Δ, a, b]

soln = sol1 /. a[_] -> 1 /. C[_] -> 1 /. a -> 0 /.
b -> 1 /. Δ -> 1;
Plot[soln /. t -> 0.01, {x, -2, 2}]

ContourPlot[soln, {x, -1, 1}, {t, 0, 1}]

The anisotropic case can be encapsulated as well:
Clear[AHeat];
AHeat[factorx_: Δx, factory_: Δy, b1_: -Infinity, b2_:Infinity,
b3_: -Infinity, b4_:Infinity] :=Module[{operator, pde2, ansatz, ptSolution, pxSolution,
pySolution, sol, sol1, sol2, pt, px, py},
operator[p_] := D[p, t] - D[factorx D[p, x], x] - D[factory D[p, y], y];
Print[{operator[f[t, x, y]] == 0, b1, b2, b3, b4} // TableForm];
ansatz = pt[t] px[x] py[y] ;
pde2 = Expand[Apply[Subtract, operator[ansatz]/ansatz == 0]];
ptSolution = First@DSolve[Select[pde2, (D[#, x] == 0 &&
D[#, y] == 0) &] == κ1^2 + κ2^2, pt[t], t];
pxSolution = First@DSolve[Select[pde2, D[#, x] =!= 0 &] == -κ1^2, px[x],
x, GeneratedParameters -> a];
pySolution = First@DSolve[Select[pde2, D[#, y] =!= 0 &] == -κ2^2, py[y],
y, GeneratedParameters -> b];
sol = ansatz /. Join[ptSolution, pxSolution, pySolution];
sol1 = Integrate[(sol /. κ1 -> I κ1), {κ1, b1,b2}];
sol2 = Integrate[(sol1 /. κ2 -> I κ2), {κ2, b3, b4}];
operator[sol1] /. factorx -> 1 /. factory -> 2 /. x -> 2 /.
y -> 3 /. t -> 3 // N // Expand // Chop // If[# != 0, Print["not ok!"]] &;
sol2]
so that
AHeat[x Δx, y Δy, 0, Infinity, 0, Infinity]

UPDATE 3
Note that mathematica does provide formal solutions in cases it cannot integrate.
For instance, this case has no closed form solution
sol1 = Heat[x + x^2, 0]

but the quadrature it returns obeys the PDE:
D[D[sol1[[1]], x] (x + x^2), x] - D[sol1[[1]], t] //Simplify// FullSimplify
(* 0 *)




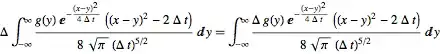
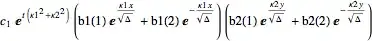



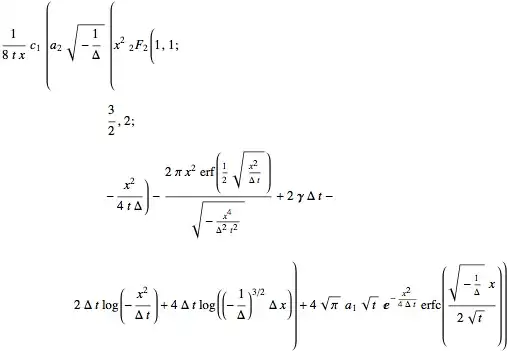



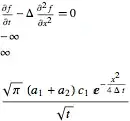
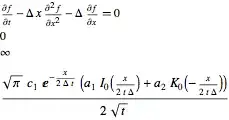















GreenFunction[PDE,BCs]would return the corresponding Green function if it is known in the literature. – chris Jul 22 '14 at 11:28FashionDatafunction. We can't be blaming WRI for not aligning their business goals with an individual's personal needs can we? – rm -rf Jul 22 '14 at 21:15DSolvecan solve heat equation now in v10.3!! – xzczd Oct 13 '15 at 07:39