Context
While studying manifold Learning I got interested in finding the eigenvectors of the Laplacian. (also in connection to this problem of solving the heat equation)
Following this and that amazing answer, I am interested in solving this Helmholtz equation in 3D
$ \triangledown^2 u(x,y,z) + k^2u(x,y,z) =0 \quad x,y,z \in \Omega\,, \quad u(x,y,z) = 0 \quad {\rm with}\quad x,y,z \in \partial\Omega $
where $\Omega =$ is some 3D boundary e.g. a ball, an ellipsoid, a regular 3D polygon etc.
I have played around with the 2D codes provided here to produce these first eigen modes of a snowflake (again beautiful code!):
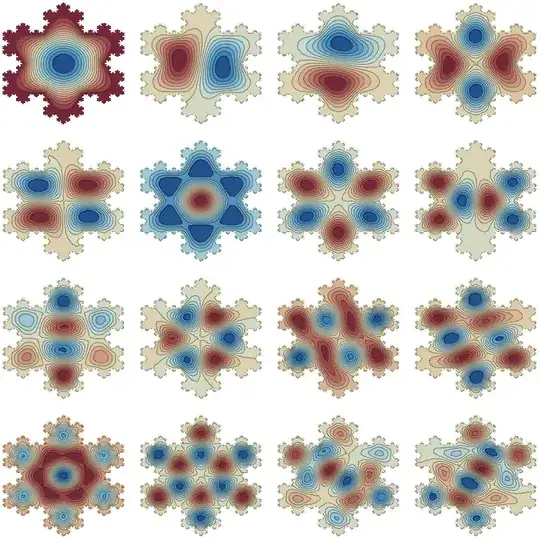
They look like this and are super-cool!
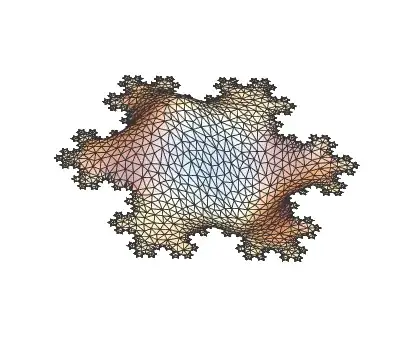
but I would like to generalize their answer to 3D.
Question
How would one proceed in 3D, given that we have a 2D solution working?
Cheeky Attempt
I have modified slightly Mark McClure's code to make it 3D savvy, but I am no expert in this field
Needs["NDSolve`FEM`"];
helmholzSolve3D[g_, numEigenToCompute_Integer,
opts : OptionsPattern[]] :=
Module[{u, x, y, z, t, pde, dirichletCondition, mesh, boundaryMesh,
nr, state, femdata, initBCs, methodData, initCoeffs, vd, sd,
discretePDE, discreteBCs, load, stiffness, damping, pos, nDiri,
numEigen, res, eigenValues, eigenVectors,
evIF},(*Discretize the region*)
If[Head[g] === ImplicitRegion || Head[g] === ParametricRegion,
mesh = ToElementMesh[DiscretizeRegion[g], opts],
mesh = ToElementMesh[DiscretizeGraphics[g], opts]];
boundaryMesh = ToBoundaryMesh[mesh];
(*Set up the PDE and boundary condition*)
pde = D[u[t, x, y, z], t] - Laplacian[u[t, x, y, z], {x, y, z}] +
u[t, x, y, z] == 0;
dirichletCondition = DirichletCondition[u[t, x, y, z] == 0, True];
(*Pre-process the equations to obtain the FiniteElementData in \
StateData*)nr = ToNumericalRegion[mesh];
{state} =
NDSolve`ProcessEquations[{pde, dirichletCondition,
u[0, x, y, z] == 0}, u, {t, 0, 1}, Element[{x, y, z}, nr]];
femdata = state["FiniteElementData"];
initBCs = femdata["BoundaryConditionData"];
methodData = femdata["FEMMethodData"];
initCoeffs = femdata["PDECoefficientData"];
(*Set up the solution*)vd = methodData["VariableData"];
sd = NDSolve`SolutionData[{"Space" -> nr, "Time" -> 0.}];
(*Discretize the PDE and boundary conditions*)
discretePDE = DiscretizePDE[initCoeffs, methodData, sd];
discreteBCs =
DiscretizeBoundaryConditions[initBCs, methodData, sd];
(*Extract the relevant matrices and deploy the boundary conditions*)
load = discretePDE["LoadVector"];
stiffness = discretePDE["StiffnessMatrix"];
damping = discretePDE["DampingMatrix"];
DeployBoundaryConditions[{load, stiffness, damping}, discreteBCs];
(*Set the number of eigenvalues ignoring the Dirichlet positions*)
pos = discreteBCs["DirichletMatrix"]["NonzeroPositions"][[All, 2]];
nDiri = Length[pos];
numEigen = numEigenToCompute + nDiri;
(*Solve the eigensystem*)
res = Eigensystem[{stiffness, damping}, -numEigen];
res = Reverse /@ res;
eigenValues = res[[1, nDiri + 1 ;; Abs[numEigen]]];
eigenVectors = res[[2, nDiri + 1 ;; Abs[numEigen]]];
evIF = ElementMeshInterpolation[{mesh}, #] & /@ eigenVectors;
(*Return the relevant information*){eigenValues, evIF, mesh}]
If I then define a 3D boundary
Ω = ImplicitRegion[0 <= x^2 + y^2 + z^2 <= 1, {x, y, z}];
RegionPlot3D[Ω, PlotStyle -> Opacity[0.5]]
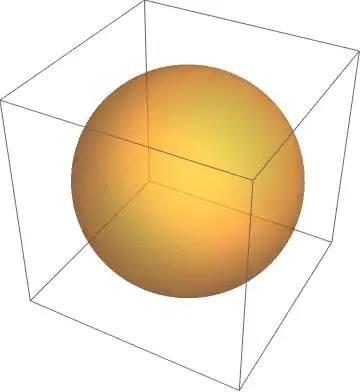
Naively this should give me the eigenmode:
{ev, if, mesh} = helmholzSolve3D[Ω, 1];
ev
but it actually crashes the kernel Mathematica (10.0.2).
Could anyone confirm this as a first step?
NB: Please do not loose sleep over this problem as it is mostly driven by curiosity :-)
PS: On the other hand I personally think this stuff is truly one of the best new useful features of Mathematica 10!














