10

I've got a Plot of a list of functions from this previous question of mine. 

rp[x_, r_] := 1000 x (r + 1)/(r + x)
ratios = Table[10^n, {n, -2, 2, 4/10}]
Plot[Map[rp[x, #] &, ratios], {x, 0, 1}, Evaluated -> True]

enter image description here

Now I want the sixth function, where ratio = 1, to be plotted with a PlotStyle -> AbsoluteThickness parameter. How can I do this?

Community
  • 1
stevenvh
  • 6,866
  • 5
  • 41
  • 64

5 Answers5

10

You can generate a list of additional style directives to go with your Plot, e.g. like this

rp[x_, r_] := 1000 x (r + 1)/(r + x)
ratios = Table[10^n, {n, -2, 2, 4/10}];
styles = If[# == 1, Thick, Thin] & /@ ratios;
Plot[Map[rp[x, #] &, ratios], {x, 0, 1}, Evaluated -> True, 
 PlotStyle -> styles]

Mathematica graphics

Yves Klett
  • 15,383
  • 5
  • 57
  • 124
10

I prefer using Style in cases like this.

rp[x_, r_] := 1000 x (r + 1)/(r + x)

ratios = Table[10^n, {n, -2, 2, 4/10}];

em = Style[#, AbsoluteThickness[4]] &;

Plot[
 MapAt[em, rp[x, #] & /@ ratios, 6],
 {x, 0, 1},
 Evaluated -> True
]

Mathematica graphics

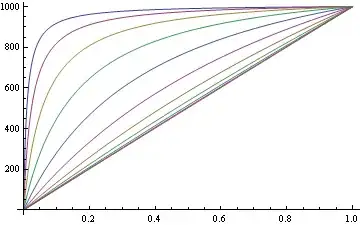
Plot[
 MapAt[em, rp[x, #] & /@ ratios, {{4}, {6}}],
 {x, 0, 1},
 Evaluated -> True
]

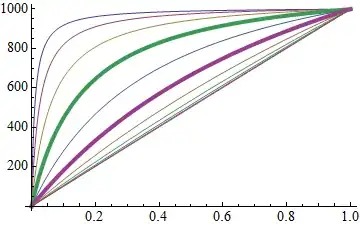
Mathematica graphics

This works for styling directives except for color (by default), but colors are overridden by the default PlotStyle colors because of the output form, which is:

Style[{(* PlotStyle directive *), Line[. . .]}, (* Style directive *)]

If for whatever reason the Style method is desirable for colors as well one could use:

red = Style[#, Red, Thick] &;

Plot[
  MapAt[red, x Range@5, {{2}, {4}}],
  {x, 1, 10},
  Evaluated -> True
] /. Style[{__, L__Line}, s__] :> Style[{L}, s]

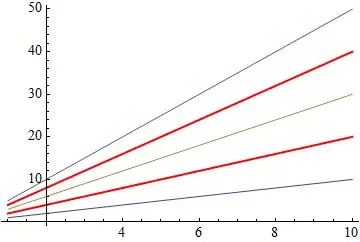
Mathematica graphics

This discards all PlotStyle directives and keeps the Style directives for lines with Style.

Mr.Wizard
  • 271,378
  • 34
  • 587
  • 1,371
  • 1
    Hi Wizard. Nice, compact code. I like it, thanks. +1 for now, later maybe more :-) – stevenvh Jul 11 '12 at 16:08
  • 3
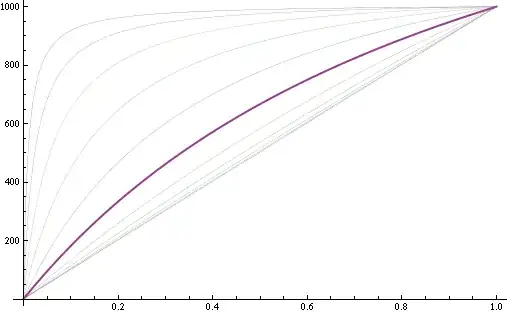
    +1, I did not know Plot accepted Style as a function. – rcollyer Jul 11 '12 at 16:57
  • 4
    @rcollyer it does, but beware that Plot's own styling overrides this so I use it only for things like Dashed and Thick, not color. – Mr.Wizard Jul 11 '12 at 17:38
  • Kudos - is this documented somewhere? – Yves Klett Jul 12 '12 at 06:33
  • You meant em (instead of style) in the last example.(+1) – kglr Jul 12 '12 at 08:59
  • @kguler thanks; I changed style to em to be less like Style, and forgot the second case. – Mr.Wizard Jul 12 '12 at 14:06
  • 2
    @YvesKlett probably so, but after years of trying I'm still not great at finding things in the Documentation system; I have sympathy for the neophytes who post "obvious" questions. – Mr.Wizard Jul 12 '12 at 14:12
  • @Mr.Wizard on the other hand I think the documentation is brimming with excellent examples and the integration of those (just evaluate in place) is way better than copy&paste orgies known from other systems/workflows. – Yves Klett Jul 12 '12 at 14:15
  • @steven thanks for the Accept; I added a supplemental example should you need it. – Mr.Wizard Jul 12 '12 at 14:28
5
 Plot[Map[rp[x, #] &, ratios], {x, 0, 1}, Evaluated -> True, 
 PlotStyle -> Map[If[#1 == 1, AbsoluteThickness[3], Automatic] &, ratios]]
kglr
  • 394,356
  • 18
  • 477
  • 896
5

In addition to Yves' answer, here's a way to modify the $n^\mathrm{th}$ line (corresponding to the $n^\mathrm{th}$ element of ratio) as a post-processing step:

Plot[Map[rp[x, #] &, ratios], {x, 0, 1}, Evaluated -> True]  /. 
    {x___, y : {Hue[__], __} ..} :> {x, MapAt[Insert[#, Thickness[Large], 2] &, {y}, 3]}

enter image description here

This modifies the 3rd line (given as the third argument of MapAt). As always, structural manipulations are made on the FullForm of the expression, so if you have a more complicated or different structure, you'll have to exploit that accordingly.

Here's the above in a Manipulate to play with:

Manipulate[
    Plot[Map[rp[x, #] &, ratios], {x, 0, 1}, Evaluated -> True] /. 
        {x___, y : {Hue[__], __} ..} :> {x, MapAt[Insert[#, Thickness[Large], 2] &, {y}, i]}, 
    {{i, 1}, 1, Length@ratios, 1}
]

enter image description here

rm -rf
  • 88,781
  • 21
  • 293
  • 472
  • ´s nice! A possible (longterm) conflict may arise if the output of Plot changes in the future. Happened to me at some major version switch and resulted in a lengthyish bug hunt ;-) – Yves Klett Jul 11 '12 at 08:13
  • Heh yeah, that's why I put in the statutory warning that it is based on the FullForm and different structures will need to be handled differently :) – rm -rf Jul 11 '12 at 08:33
  • The severability clause is (and was) duly noted. Just wanted to drive the point home ´cause a thing like this once came back and bit me ;-) – Yves Klett Jul 11 '12 at 08:55
  • @YvesKlett it only bit you once? Lucky. I've got code written for 4 major releases, and I pray every time I have to run something from an older version. Of course, some of the prayer is due to the difference in coding ability between then and now, but I digress. :) – rcollyer Jul 11 '12 at 16:56
  • @rcollyer not once, alas, but hacky solutions tend to HCF just a bit more often and then you cannot even blame WRI... – Yves Klett Jul 12 '12 at 07:07
  • 1
    @YvesKlett my wife actually had a computer catch fire while she was using it. – rcollyer Jul 12 '12 at 11:37
  • @rcollyer hot darn! A real power user, then ;-) My graphics card sometimes also seems to be responsible for a nontrivial part global warming (thank you, CUDA). – Yves Klett Jul 12 '12 at 13:37
3

I'm on Linux and using Yves excellent answer I get the following output:

Mathematica graphics

which has a very high contrast between the emphasised line and the rest.

Using a combination of thick and dashed lines seems to my eye to give more pleasing result:

rp[x_, r_] := 1000 x (r + 1)/(r + x)
ratios = Table[10^n, {n, -2, 2, 4/10}];
styles = If[# == 1, Thick, Dashed] & /@ ratios;
Plot[Map[rp[x, #] &, ratios], {x, 0, 1}, Evaluated -> True, 
 PlotStyle -> styles]

Mathematica graphics

image_doctor
  • 10,234
  • 23
  • 40