Finding where two parametric paths cross?

Question

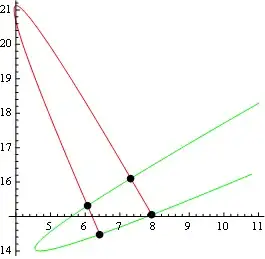
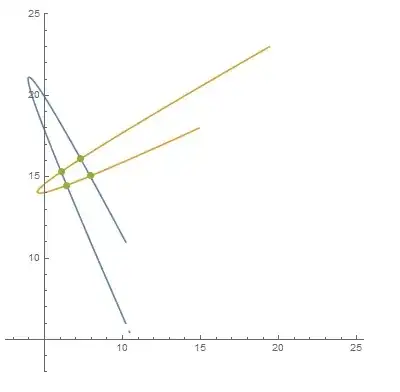
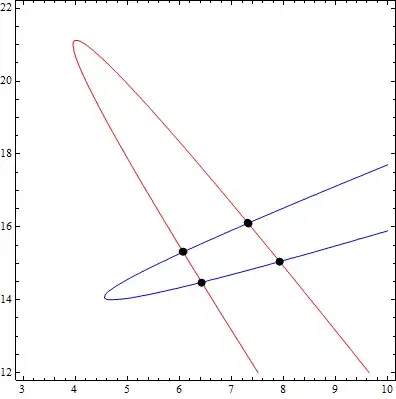
I have been looking through other parametric equations questions and am still unsure where to start with this one. I am given two functions:

f[t_] = {16.2 - 7 t + t^2, 13 t - 2 t^2};
g[t_] = {26 - 13.1 t + 2 t^2, 23 - 6 t + t^2};

How do I show where these two parametric paths cross? How would I simplify these two sets? Thank you!

Answer 1

If they don't need to cross at the same $t$, then you can solve

Solve[f[t1] == g[t2], {t1, t2}]

since they are polynomials. Otherwise, you might use FindRoot. This yields a set of four solutions. You can then plug these pairs of t1 and t2 back into your expressions for f and g to get the actual points where the curves cross.

Answer 2

f[t_] := {16.2 - 7 t + t^2, 13 t - 2 t^2};
g[t_] := {26 - 13.1 t + 2 t^2, 23 - 6 t + t^2};

sols = Transpose[{t, t1} /. NSolve[f@t == g@t1, {t, t1}]]
p[f_, c_] := ParametricPlot[f[t], Evaluate@{t, Sequence @@ ({Max@#, Min@#} &@sols)}, 
                            PlotRange -> All,  PlotStyle -> c]

Show[p[f, Red], p[g, Green], Graphics[{PointSize[Large], Point[f /@ sols[[1]]]}], 
     AspectRatio -> 1]

Answer 3

Attacking the problem from a different point of view:

f[t_] = {16.2 - 7 t + t^2, 13 t - 2 t^2};
g[t_] = {26 - 13.1 t + 2 t^2, 23 - 6 t + t^2};

pts = NSolve[Thread[f[t1] == g[t2]], {t1, t2}]

{{t1 -> 5.07271, t2 -> 2.30684}, {t1 -> 4.95465, t2 -> 4.146}, 
 {t1 -> 1.66574, t2 -> 4.45096}, {t1 -> 1.50689, t2 -> 1.97621}}

Show[ContourPlot[Evaluate@Thread[f[t1] == g[t2]], {t1, 0, 6}, {t2, 0, 6}, 
      FrameLabel -> Automatic], 
     Graphics[{Red, PointSize[Large], Point[{t1, t2} /. pts]}]]

Answer 4

If you are looking just to show them then you can also use RegionIntersection

r1 = ParametricRegion[f[t], {{t, 1, 6}}];
r2 = ParametricRegion[g[t], {{t, 1, 6}}];
int = RegionIntersection[r1, r2];

RegionPlot[{r1, r2, int}, Frame -> False, Axes -> True, 
 PlotRange -> {3, 25}, BoundaryStyle -> {PointSize[0.02]}]

Answer 5

Just post as another method.

Considering the two parametric equations are polynomials，we can obtain the implicit equation by eliminate the parametric $t$.

Using the function GroebnerBasis.

f[x_, y_] := 
  Evaluate@GroebnerBasis[{x - (162/10 - 7 t + t^2), 
    y - (13 t - 2 t^2)}, {t, x, y}][[1]];
g[x_, y_] := 
  Evaluate@GroebnerBasis[{x - (26 - 131/10 t + 2 t^2), 
    y - (23 - 6 t + t^2)}, {t, x, y}][[1]]

Then plot the two curves and their cross points.

ContourPlot[{f[x, y] == 0, g[x, y] == 0}, {x, 3, 10}, {y, 12, 22}, 
 ContourStyle -> {Red, Blue}, Mesh -> {{0, 0}}, 
 MeshFunctions -> {f[#1, #2] &, g[#1, #2] &}, 
 MeshStyle -> Directive[PointSize[Large], Black]]