You can combine parts of @Julian comment and @Szabolcs comment in the original post to have it marked automatically.
f[x_] := (2^x - 2)/(x - 1)
Plot[f[x], {x, -10, 10},
Exclusions -> {Reduce[! FunctionDomain[f[x], x]]},
ExclusionsStyle -> {Disk[], PointSize -> 0.015`}]
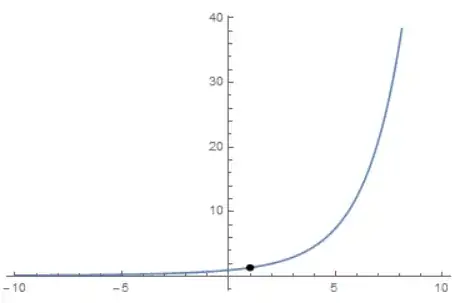
The inequalities that are returned by FunctionDomain negated to get the region not in the function's domain. The Reduce is used to combine inequalities where needed. Exclusions prevents points in the region from being plotted and ExclusionsStyle marks the points.
Hope this helps.
Update
Try it with Manipulate.
Manipulate[
Plot[h[x], {x, -10, 10},
Exclusions -> {Quiet@Reduce[! FunctionDomain[h[x], x]]},
ExclusionsStyle -> {Disk[], PointSize -> 0.015`},
PlotRange -> {{-10, 10}, Automatic}],
{{c, 1}, -9.5, 9.5},
Initialization :> {h[x_] := (2^x - 2)/(x - c);},
TrackedSymbols :> {c}]


– Julian Jul 12 '15 at 21:23Plot[f[x], {x, -10, 10}, Exclusions -> {x == 1}, ExclusionsStyle -> {Disk[], PointSize -> 0.015}]FunctionDomaincan be useful to try to detect points like these. Generally, I don't think there's a good automatic and reliable way to detect such points though. – Szabolcs Jul 12 '15 at 21:26((x - 1) (x - 2))/(x - 1)and won't care about the fact that technically that function should be undefined atx==1. Trying to handle these details would make them much too impractical and probably slow. The conclusion is: it is up to you do decide whether you consider that function defined at x==1 or not, in the strict mathematical sense, and keep this in mind during symbolic manipulations. Mathematica will ignore ... – Szabolcs Jul 12 '15 at 22:02FunctionDomainthat I suggested? – Szabolcs Jul 12 '15 at 22:03Solve[Denominator[f[x]] == 0, x]– Bob Hanlon Jul 12 '15 at 22:05FunctionDomain. I was just wondering if there was an automatic way to do it but I've read your answer to the question in the link and it seems it's not possible. I now know there are practical reasons for that. Thank you for your comments and for the link. – Cristopher Jul 12 '15 at 22:16Piecewise, an oversight on my part. But it will handle the OP's example automatically (if wrapped inPiecewise): http://i.stack.imgur.com/BRhMD.png – Michael E2 Jul 13 '15 at 04:04