Help remove annoying vertical lines in a piecewise plot

Question

I use the following codes to define and plot three piecewise functions.

list1 = Join[
   Table[{(j - 1)/2^1, (j - 1)/2^1 <= E^x < j/2^1}, {j, 1, 
     1*2^1}], {{1, E^x >= 1}}];
list2 = Join[
   Table[{(j - 1)/2^2, (j - 1)/2^2 <= E^x < j/2^2}, {j, 1, 
     2*2^2}], {{2, E^x >= 2}}];
list3 = Join[
   Table[{(j - 1)/2^3, (j - 1)/2^3 <= E^x < j/2^3}, {j, 1, 
     3*2^3}], {{3, E^x >= 3}}];
p1 = Piecewise[list1];
p2 = Piecewise[list2];
p3 = Piecewise[list3];

Plot[p1, {x, -3, 3}, AspectRatio -> Automatic]
Plot[p2, {x, -3, 3}, AspectRatio -> Automatic]
Plot[p3, {x, -3, 3}, AspectRatio -> Automatic]

p1 and p2 just come out fine, while p3 is messy, with end points of each horizontal lines connected by vertical lines.

Thank you!

Related, possible duplicates: (8576), (10501), (11714) – Mr.Wizard Jul 23 '15 at 20:41 — Mr.Wizard, Jul 23 '15 at 20:41

score 6 · Accepted Answer · edited Apr 13 '17 at 12:55

6

Using @Rojo's answer to my question here you don't need to know a priori where the exclusions are:

plot = Plot[p3, {x, -3, 3}, PlotPoints -> 1000];

pp = With[{multiplier = {AspectRatio, PlotRange} /. 
     AbsoluteOptions[plot, {AspectRatio, PlotRange}] /. {ar_, pl_} :> 
                             ar Divide @@ Subtract @@@ Reverse /@ pl}, 
  (plot //. 
   Line[{a___, {x1_, y1_}, {x2_, y2_}, b___}] /; 
     Abs[(y1 - y2)/(x1 - x2)] > 10/multiplier :> {Line[{a, {x1, y1}}],
      Line[{{x2, y2}, b}]})
 ];

Show[pp, AspectRatio -> Automatic]

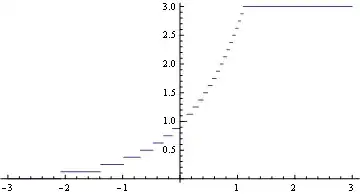
Mathematica graphics

edited Apr 13 '17 at 12:55

Community

1

answered Jul 23 '15 at 19:34

Dr. belisarius

115,881
13
203
453

Do you feel this question can be marked as a duplicate of (10501)? – Mr.Wizard Jul 23 '15 at 20:41
@Mr.Wizard Not exactly that one.Here we are talking specifically about Piecewise[ ] which may allow some messing with the Piecewise[ ] specificities if someone else care to do it. – Dr. belisarius Jul 23 '15 at 20:45
Okay, good point. – Mr.Wizard Jul 23 '15 at 20:47

Michael E2 · Answer 2 · 2015-07-24T11:40:05.297

The problem is that to find the discontinuities, Plot internally calls

PiecewiseExpand[p3, Method -> {"OrderlessConditions" -> True}]

but with a time constraint of 0.2 seconds. (See PiecewiseExpand for an explanation of the option.) Because of the somewhat complicated conditions on x -- ok, inequalities in terms of E^x may not seem that complicated to a good high school student, but Mathematica apparently thinks so -- it takes much, much more time than that. The time constraint 0.2 seems to be hard-coded, so we cannot easily approach the problem from that angle. A better way is to simplify the function first using Reduce to get the inequalities in terms of x:

PiecewiseExpand[p3, Method -> {"ConditionSimplifier" -> (Reduce[#, x, Reals] &)}]

Then we get

Plot[Evaluate@
  PiecewiseExpand[p3, Method -> {"ConditionSimplifier" -> (Reduce[#, x, Reals] &)}],
 {x, -3, 3}, AspectRatio -> Automatic, 
 PlotPoints -> 200, Exclusions -> All]

Mathematica graphics

Evaluating the PiecewiseExpand before passing it to Plot, either using another variable to store the result or using Evaluate as above, is necessary. Otherwise the internal call to PiecewiseExpand will be made on the input PiecewiseExpand[p3,...], which will take longer than 0.2 seconds. In that case, the discontinuity processing fails and you get the annoying vertical lines.

Update:

The point of the option "OrderlessConditions" -> True is the reduce the conditions to non-overlapping intervals. The irony is that p3 already satisfies that criterion. So we can mimic the internal processing of the discontinuities, which is faster than simplifying them with reduce:

excl = With[{p = p3[[1, All, 2]]},
   Thread[
    (LogicalExpand /@ p /.
       {f_ <= g_ :> f - g, f_ < g_ :> f - g, f_ >= g_ :> g - f, f_ > g_ :> g - f, 
        And -> Max}) == 0
    ]
   ];
Plot[p3, {x, -3, 3}, AspectRatio -> Automatic, PlotPoints -> 200, 
 Exclusions -> excl]

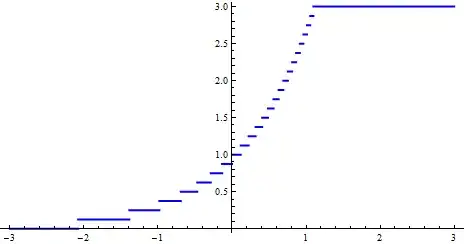
The plot looks the same.

I wonder if the Villegas-Gayley trick is usable here to thwart the arbitrary time constraint… — J. M.'s missing motivation, Jul 24 '15 at 12:44
@J. M. I thought about that, but setting the time to 600 seconds still failed. — Michael E2, Jul 24 '15 at 13:09
@J. M. Basically, the time complexity of PiecewiseExpand[p3, Method -> {"ConditionSimplifier" -> (Reduce[#, x, Reals] &)}] in this case seems to be roughly proportional to $2^n$, where $n$ is the number of pieces in p3. — Michael E2, Jul 24 '15 at 17:17
"Exponential in the number of pieces" is indeed slow… indeed, it does seem best to preprocess your discontinuous function before feeding it to Plot[]. — J. M.'s missing motivation, Jul 24 '15 at 17:21
@J. M. Oops, I meant the option "OrderlessConditions" -> True. Oh, bother.... — Michael E2, Jul 24 '15 at 17:25

george2079 · Answer 3 · 2015-07-23T20:26:54.020

3

 Plot[p3, {x, -3, 3}, 
      Exclusions -> Table[Exp[x] == j/2^3, {j, 1, 3*2^3}], 
       PlotPoints -> 1000]

or if you don't know where the jumps are:

 ListPlot[GatherBy[Table[{x, p3}, {x, -3, 3, .01}], #[[2]] &],
     Joined -> True, PlotStyle -> Blue]

this could be extended with a tolerance as, Gather[ .. , Abs[#1[[2]]-#2[[2]] ]< eps & ]

edited Jul 23 '15 at 20:26

answered Jul 23 '15 at 19:36

george2079

38,913
1
43
110

score 3 · Answer 4 · answered Jul 23 '15 at 21:00

3

Plot[Evaluate[ConditionalExpression @@@ list3], {x, -3, 3}, 
 AspectRatio -> Automatic, PlotStyle -> Blue, BaseStyle -> Thick, PlotPoints -> 200]

Mathematica graphics

answered Jul 23 '15 at 21:00

kglr

394,356
18
477
896

score 1 · Answer 5 · answered Jul 23 '15 at 23:19

1

In 10.2 there is ListStepPlot.

ListStepPlot[Table[{t, p3 /. x :> t}, {t, -3, 3, 0.001}], Joined -> False]

Hope this helps.

answered Jul 23 '15 at 23:19

Edmund

42,267
3
51
143

Help remove annoying vertical lines in a piecewise plot

5 Answers5

Linked