Plot of the Mod of NDSolve solutions sometimes connects discontinuous jumps

Question

UPDATE 2: Fixed in V11!

UPDATE: The answers given are informative, and provide a workaround which has been given in other posts, but is unfortunately not very efficient. There still seems to be a lack of deeper understanding of the origin of the problem, and of a solution which might address the problem more directly and/or efficiently. So I'm choosing to keep the question open in the hopes of still receiving such an answer.

---

I've had trouble plotting periodic solutions to NDSolve properly. By periodic I mean solutions that I have modified with Mod[ ] (after receiving them from NDSolve) so that they're subjected to periodic boundary conditions.

The trouble is that sometimes when the solution "jumps" from one side of the plot to the other (due to the periodic boundary conditions), the plot draws a straight line from one point to the next, crossing the entirety of the graph.

After eliminating other known causes of this, I've found that it is reproducible only for particularly "difficult" solutions. In my case, the equations being solved have to be several coupled nonlinear equations, and the length in time of the solution must be past some (inconsistent) threshold.

Example:

The following code solves for position and momentum of a particle's motion in 2D space, using {x'[t] == 2 px[t], px'[t] == Sin[x[t]], y'[t] == 2 py[t], py'[t] == Sin[y[t]]} with simple initial conditions, going from t=0 to some t=tmax. It then plots two forms of the solution:

1. The spatial solution made periodic on a rectangle by using Mod[ ] on x and y
2. The spatial solution made periodic on a diamond shape by using Piecewise on x and y (the details are a little subtle but unnecessary for this question)

Note that the details of this example are likely irrelevant to the problem, but since the problem requires a somewhat complex case for it to occur, it was hard to simplify any further.

Here's the code:

x=1;

Clear[x1, px1, y1, py1, s1, x, px, y, py]

tmax = 40;

s1 = NDSolve[{x'[t] == 2 px[t], px'[t] == Sin[x[t]], y'[t] == 2 py[t],
     py'[t] == Sin[y[t]], x[0] == 0, px[0] == 1, y[0] == π, 
     py[0] == 1}, {x, px, y, py}, {t, 0, tmax}, MaxSteps -> 10000000][[1]];

(*x1 etc. are solutions with a rectangular boundary*)
x1[t_] = Mod[Evaluate[x[t] /. s1], 4 π, -2 π];
px1[t_] = Evaluate[px[t] /. s1];
y1[t_] = Mod[Evaluate[y[t] /. s1], 4 π/Sqrt[3]];
py1[t_] = Evaluate[py[t] /. s1];

(*x etc. are solutions on a diamond boundary*)
x[t_] = Piecewise[{{x1[t] - 2 π, 
     y1[t] > 4 π/Sqrt[3] - x1[t]/Sqrt[3]},(*move NE corner*)
    {x1[t] - 2 π, y1[t] < x1[t]/Sqrt[3]},(*move SE corner*)
    {x1[t] + 2 π, y1[t] > 4 π/Sqrt[3] + x1[t]/Sqrt[3]},(*move NW corner*)
    {x1[t] + 2 π, y1[t] < -x1[t]/Sqrt[3]}},(*move SW corner*)
     x1[t]];

px[t_] = px1[t];

y[t_] = Piecewise[{{y1[t] - 2 π/Sqrt[3], 
     y1[t] > 4 π/Sqrt[3] - x1[t]/Sqrt[3]},(*move NE corner*)
    {y1[t] + 2 π/Sqrt[3], y1[t] < x1[t]/Sqrt[3]},(*move SE corner*)
    {y1[t] - 2 π/Sqrt[3], y1[t] > 4 π/Sqrt[3] + x1[t]/Sqrt[3]},(*move NW corner*)
    {y1[t] + 2 π/Sqrt[3], y1[t] < -x1[t]/Sqrt[3]}},(*move SW corner*)
     y1[t]];

py[t_] = py1[t];

modplot = 
 ParametricPlot[{x1[t], y1[t]}, {t, 0, 5}, AxesOrigin -> {0, 0}, 
  PlotStyle -> RGBColor[0, 0, 0], AspectRatio -> 1/Sqrt[3], 
  PlotRange -> {{-2 π, 2 π}, {0, 4 π/Sqrt[3]}}, 
  PlotLabel -> "Rectangular Periodic BC's, t=40"]

diamondplot = 
  ParametricPlot[{x[t], y[t]}, {t, 0, 5}, AxesOrigin -> {0, 0}, 
   PlotStyle -> RGBColor[0, 0, 0], AspectRatio -> 1/Sqrt[3], 
   PlotRange -> {{-2 π, 2 π}, {0, 4 π/Sqrt[3]}}, 
   PlotLabel -> "Diamond Periodic BC's, t=40"];

diamondbg = {Plot[x/Sqrt[3], {x, 0, 2 \[Pi]}, PlotStyle -> RGBColor[1, 0, 0]], 
   Plot[-x/Sqrt[3], {x, -2 π, 0}, PlotStyle -> RGBColor[0, 0, 1]],
   Plot[4 π/Sqrt[3] - x/Sqrt[3], {x, 0, 2 π}, PlotStyle -> RGBColor[0, 0, 1]], 
   Plot[4 π/Sqrt[3] + x/Sqrt[3], {x, -2 π, 0}, PlotStyle -> RGBColor[1, 0, 0]]};

Show[diamondplot, diamondbg]

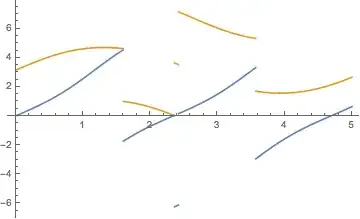
When tmax is low (I used tmax = 40 here), the plots look the way they should, like this:

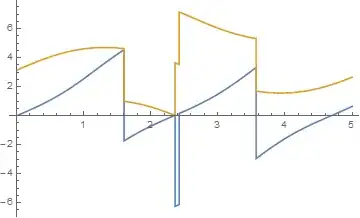
But when tmax is high (for me tmax=80 did the trick), the latter graph gets some inconvenient black lines strewn across it:

The lines seem to be NDSolve choosing to line-connect all the points in the solution, thereby connecting parts of the solution that should be physically separated by the boundary conditions. And this seems to happen once the solution passes a certain (unclear) level of complexity. This threshold of complexity is also inconsistent, as I sometimes find that when using tmax = 60, one run will produce the lines while the next run (with nothing altered) will not.

(As a guess for why this alteration happens at all, I have noticed that in general some NDSolve solutions have outright gaps where the solution path is briefly disconnected, so this may be an attempt to self-correct those kinds of errors.)

So my question is: How can I force NDSolve to never produce these lines? Is there an option that can be set for this?

Answer 1

Update: This problem seems to have been fixed in V11.

---

This question is related to my answer to Help remove annoying vertical lines in a piecewise plot.

The discontinuity processing is done under a time constraint of 0.2 seconds. When NDSolve is run for over a longer interval, the results take up more memory and take longer for Plot to process. At some point, the time exceeds the constraint and Plot skips the automatic Exclusions processing.

Using bbgodfrey's simplified code, with tmax set to 40 and 300 resp., here are the timings for analyzing the exclusions:

foo40 = Visualization`VisualizationDiscontinuities[x2[t], {t}]; // Timing
(*  0.0392754  *)

foo300 = Visualization`VisualizationDiscontinuities[x2[t], {t}]; // Timing
(*  0.301278  *)

As you can see, the larger solution takes much longer. Here are the sizes of the solutions:

ByteCount@ {x2[t], y2[t]}   (* tmax = 40 *)
(*  397784  *)

ByteCount@ {x2[t], y2[t]}   (* tmax = 300 *)
(*  2739256  *)

A possible, but slow, workaround is

Plot[{x2[t], y2[t]}, {t, 0, 5}, PlotPoints -> 100, Exclusions -> foo300[[All, 2]]]

If the discontinuities of x2 and y2 were different, you would have to compute each and join them.

Edit: Addendum

Note that for ParametricPlot, the call is on the whole parametrization:

Visualization`VisualizationDiscontinuities[{x2[t], y2[t]}, {t}]

Plot calls VisualizationDiscontinuities separately. In all cases, the time constraint is 0.2. While the call on the whole parametrization took only a little longer than a call on a single component, it is nonetheless probably the reason why results are difficult to replicate, since the time a computation takes might vary from machine to machine.

Answer 2

As a starting point for addressing this rather difficult question, it makes sense to omit as much code as possible while still reproducing the issue.

tmax = 40;
{x0, y0} = NDSolveValue[{x'[t] == 2 px[t], px'[t] == Sin[x[t]], y'[t] == 2 py[t],
     py'[t] == Sin[y[t]], x[0] == 0, px[0] == 1, y[0] == π, 
     py[0] == 1}, {x, y}, {t, 0, tmax}, StartingStepSize -> 10^-4];
x1[t_] = Mod[x0[t], 4 π, -2 π];
y1[t_] = Mod[y0[t], 4 π/Sqrt[3]];
x2[t_] = x1[t] - 2 π Piecewise[{{1, ! (4 π - x1[t] > Sqrt[3] y1[t] > x1[t])},
    {-1, ! (4 π + x1[t] > Sqrt[3] y1[t] > -x1[t])}}];
y2[t_] = y1[t] - 2 π/Sqrt[3] Piecewise[{{1, ! (4 π - Sqrt[3] y1[t] > x1[t] > 
    Sqrt[3] y1[t] - 4 π)}, {-1, ! (Sqrt[3] y1[t] > x1[t] > -Sqrt[3] y1[t])}}];

This abbreviated code differs from that in the question in one substantive way. StartingStepSize -> 10^-4 has been added to the options of NDSolveValue to assure that the temporal grid for small t is independent of tmax. Although this change has no direct effect on the issue at hand, it is essential for the comparisons made later in this answer. To see that the code in this answer produces substantially the same results as those in the question, use

ParametricPlot[{x1[t], y1[t]}, {t, 0, 5}, AxesOrigin -> {0, 0}, 
                AspectRatio -> 1/Sqrt[3], PlotRange -> {{-2 π, 2 π}, {0, 4 π/Sqrt[3]}}]

which reproduces the first plot in the question, and

ParametricPlot[{x2[t], y2[t]}, {t, 0, 5}, AxesOrigin -> {0, 0}, 
                AspectRatio -> 1/Sqrt[3], PlotRange -> {{-2 π, 2 π}, {0, 4 π/Sqrt[3]}}]

which reproduces the second plot in the question, but without the diamond-shaped boarder. Likewise, creating these same plots for tmax = 300 (for instance) yields the third and fourth plots in the question, again without the diamond-shaped boarder. However, it is more informative to consider, instead,

Plot[{x2[t], y2[t]}, {t, 0, 5}, PlotPoints -> 100]

which for tmax = 40 yields

and for tmax = 300 yields

Plot should, and usually does, eliminate the vertical lines at function discontinuities but does not do so here at tmax = 300 and other large values of tmax. Adding the option Exclusions -> True in Plot does not help. Of course, setting Exclusions to the list of t values at which the discontinuities occur would eliminate the vertical lines, but doing so does not address the issue of why Plot eliminate the vertical lines for some tmax and not others.

The obvious hypothesis is that x0 and y0, and the quantities derived from them, differ in the plot domain, 0 <= t <= 5 for different tmax. To test this supposition, we first compare the actual values of x0 and y0 computed by NDSolveValue on the temporal grid 0 <= t <= 5.66. (For convenience, x0, etc are labeled x0b for tmax = 40 in what follows, while x0, etc are the quantities for tmax = 300.)

Transpose[{Flatten[x0["Grid"]], Flatten[x0["ValuesOnGrid"]], 
    Flatten[y0["ValuesOnGrid"]]}][[1 ;; 120]] == 
 Transpose[{Flatten[x0b["Grid"]], Flatten[x0b["ValuesOnGrid"]], 
    Flatten[y0b["ValuesOnGrid"]]}][[1 ;; 120]]
(* True *)

They are the same for 0 <= t <= 5.66. In fact, more information lurks in the InterpolatingFunctions produced by NDSolveValue,

x0b[[4, 3]][[1 ;; 240]] == x0[[4, 3]][[1 ;; 240]]
y0b[[4, 3]][[1 ;; 240]] == y0[[4, 3]][[1 ;; 240]]
(* True *)
(* True *)

But these too are the same. Evaluating the functions themselves at thousands of points also uncovers no differences.

Table[{i, x1[i], y1[i], x2[i], y2[i]}, {i, 0, 5.66, .001}] == 
    Table[{i, x1b[i], y1b[i], x2b[i], y2b[i]}, {i, 0, 5.66, .001}]
(* True *)

Furthermore, Maximize is unable to find any differences; e.g.,

Maximize[{Abs[x2[t] - x2b[t]], 0 < t < 5}, t]
(* {0., {t -> 0.71765}} *)

(I also have examined the Line instructions inside the Plots, but they appear to yield no useful additional information.)

I can only conclude that whether Plot automatically can find discontinuities depends on details of the InterpolatingFunctions well outside the domain of the plot. Further investigation of this issue appears to require information not generally available to Mathematica users. Incidentally, the undesirable lines in the ParametricPlots occur whenever they occur in the corresponding Plots, and sometimes even when they do not occur in the corresponding Plots. Evidently, ParametricPlot has more difficulty identifying discontinuities than Plot does, which seems strange.