Here's a solution using Lua. It isn't perfect, I assumed the main coefficient is 1 and I wasn't very careful with rounding floating values, but it should be easy to tweak to your needs.
\documentclass{article}
\usepackage{luacode}
\begin{luacode}
-- Computes the roots of x^2+bx+c=0
-- Returns nothing if they aren't real
function roots(b, c)
local delta = bb-4c
if delta > 0 then
deltasq = math.sqrt(delta)
local r1 = math.round((-b-deltasq)/2)
local r2 = math.round((-b+deltasq)/2)
return r1, r2
end
end
-- Outputs x^2+bx+c in developed form to LaTeX
function display_polynome(b, c)
p = "x^2"
if b > 0 then
p = p .. "+" .. tostring(b) .. "x"
elseif b < 0 then
p = p .. tostring(b) .. "x"
end
if c > 0 then
p = p .. "+" .. tostring(c)
elseif c < 0 then
p = p .. tostring(c)
end
tex.print(p)
end
-- Outputs x^2+bx+c in factorized form to LaTeX
function display_factorized_polynom(b, c)
r1, r2 = roots(b, c)
p = "(x"
if r1 > 0 then
p = p .. "-" .. tostring(r1) .. ")(x"
elseif r1 < 0 then
p = p .. "+" .. tostring(-r1) .. ")(x"
end
if r2 > 0 then
p = p .. "-" .. tostring(r2) .. ")"
elseif r2 < 0 then
p = p .. "+" .. tostring(-r2) .. ")"
end
tex.print(p)
end
\end{luacode}
\begin{document}
$\directlua{display_polynome(2, -15)}$
$\directlua{display_factorized_polynom(2, -15)}$
\end{document}
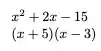
Bonus points if you're using VS Code, as it switches to Lua syntax highlighting in luacode environments.
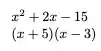

\showex{-5}{3}as it is easy to generate all your display from there. If instead you start from the polynomial, it is harder to parse and harder to process, and more cases, complex roots etc – David Carlisle Jul 02 '22 at 15:38