How to solve a system of PDEs with zip condition?

Question

I have a system of PDEs in the following form,

$$\frac{\partial T_1}{\partial t}=\frac{\partial^2 T_1}{\partial x^2},\,\,0<x<S(t)$$ with $T_1(x,0)=-10,\,\,T_1(0,t)=-10,\,\, T_1(S(t),t)=10$, and $$\frac{\partial T_2}{\partial t}+\frac{dS(t)}{dt}\frac{\partial T_2}{\partial x}=\frac{\partial^2 T_2}{\partial x^2},\,\,x>S(t)$$ with $T_2(x,0)=10,\,\,T_2(S(t),t)=10,\,\, T_2(20,t)=20$.

The above two equations are zip together by $$\frac{dS(t)}{dt}=\frac{\partial T_1}{\partial x}\Biggl|_{x=S(t)}-\frac{\partial T_2}{\partial x}\Biggl|_{x=S(t)}$$ with $S(0)=0$.

Eq1 = D[T1[x, t], t] == D[T1[x, t], x, x]
Eq2 = D[T2[x, t], t]+D[S[t], t] D[T2[x, t], x]== D[T2[x, t], x, x]
T1[x, 0] == -10,T1[0,t] == -10, T1[S(t), t] == 10,T2[x, 0] == 10,T2[S(t), t] == 10,T2[20, t] == 20

Is there a way to solve the above system in Mathematica?

Answer 1

This problem is quite similar to PDE with Stefan Conditions, a.k.a variable boundary, and can be solved more easily because now we have DChange and pdetoode.

We first use DChange to transform $T_1(x_1,t)$ and $T_2(x_2,t)$ to $T_1(\xi,t)$ and $T_2(\xi,t)$, where

$$\frac{x_1}{S(t)}=\xi$$ $$\frac{x_2-S(t)}{20-S(t)}=\xi$$

xR = 20;
eqL = D[T1[x, t], t] == D[T1[x, t], x, x];
eqR = D[T2[x, t], t] + D[S[t], t] D[T2[x, t], x] == D[T2[x, t], x, x];
{icL, icR} = {T1[x, 0] == -10, T2[x, 0] == 10};
{bcL, bcR} = {{T1[0, t] == -10, T1[S@(t), t] == 10}, 
              {T2[S@(t), t] == 10, T2[xR, t] == 20}};
slopeL = (D[T1[x, t], x] /. x -> S[t]);
slopeR = (D[T2[x, t], x] /. x -> S[t]);
bcmidfunc = S'[t] == # - #2 &;
With[{eps = 10^-10}, icmid = S[0] == eps];
(* Definition of DChange isn't included in this code piece,
   please find it in the link above *)
changeL = DChange[#, x/S@t == ξ, x, ξ, T1[x, t]] &;
changeR = DChange[#, (x - S[t])/(xR - S[t]) == ξ, x, ξ, T2[x, t]] &;
(* Definition of diffbc isn't included in this code piece,
   please find it in the link above *)
toode = With[{sf = 100}, diffbc[t, sf]];
{neweqL, newicL, newbcL, newslopeL} = 
 changeL@{eqL, icL, toode@bcL, slopeL} /. S[0] -> S[t]
{neweqR, newicR, newbcR, newslopeR} = 
 changeR@{eqR, icR, toode@bcR, slopeR} /. S[0] -> S[t] // Simplify

Remark

1. The /. S[0] -> S[t] is added because currently DChange can't handle coefficients involving the independent variable very well.

2. Check this post if you don't understand why we need toode.

After the change of variable, $T_1$ and $T_2$ are both defined in $[0,1]\times[0,t_{end}]$, while $S$ is defined in $[0,t_{end}]$, so NDSolve still can't solve the equation set directly. We need to discretize the PDEs to a set of ODEs. I'll use pdetoode for the task:

points = 25;
xdifforder = 4;
{ξL, ξR} = domain = {0, 1};
grid = Array[# &, points, domain];
(* Definition of pdetoode isn't included in this code piece,
   please find it in the link above *)
ptoo = pdetoode[{T1, T2}[ξ, t], t, grid, xdifforder];
del = #[[2 ;; -2]] &;
{odeL, odeicL, odebcL, odeslopeL, odeR, odeicR, odebcR, odeslopeR} = 
    MapAt[del, ptoo /@ {neweqL, newicL, newbcL, newslopeL, neweqR, newicR, newbcR, 
          newslopeR}, {{1}, {5}}];
odebcmid = bcmidfunc[odeslopeL, odeslopeR]
odeicmid = icmid;
tend = 40;
sollst = NDSolveValue[{odeL, odeR, odeicL, odeicR, odebcL, odebcR, 
        odebcmid, odeicmid}, {T1 /@ grid, T2 /@ grid, S}, {t, 0, tend}];
solL = rebuild[#, grid, -1]&@sollst[[1]];
solR = rebuild[#, grid, -1]&@sollst[[2]];
solS = sollst[[-1]];
sol = {x, t} [Function] 
      Piecewise[{{solL[x/solS@t, t], ξL <= x/solS@t <= ξR}}, 
        solR[(x - solS[t])/(xR - solS[t]), t]];
Manipulate[Plot[sol[x, t], {x, 0, xR}, PlotRange -> {-10, 20}], {t, 0, tend}]
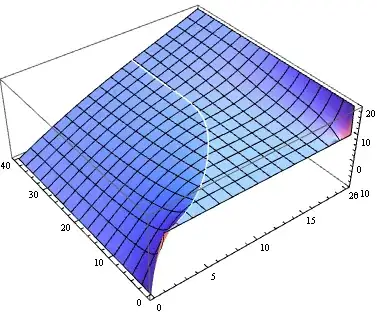
(* Plot3D[sol[x, t], {x, 0, xR}, {t, 0, tend}, PlotRange -> {-10, 20}, 
   PlotPoints -> 50] *)