On the original question of how to solve classic Stefan-type problems using NDSolve with its high-level syntax (referred to in the posts as 'automatically'). This can be done. Essentially, first reformulate the problem as an optimal stopping problem: see van Moerbeke, Rocky Mountain J. Math. 4(3), 539-578, 1974.
This leads to problems very similar to early exercise problems in Mathematical Finance. To solve these types of problems automatically with NDSolve, you can employ the WhenEvent methodology. Details are found in my recent book, "Option Valuation under Stochastic Volatility II", including a classic Stefan problem example. In Chapter 9, I treat a Stefan-type problem that is similar to, but not identical to the original question, namely:
$$ \begin{align}
w_{\tau} &= \frac{1}{2} w_{xx}, \quad x \in (s(\tau),\infty), \\
w(x,0) &= k \, 1_{\{x \ge 0 \}}, \quad (k > 0), \\
w(s(\tau),\tau) &= 0, \\
w_x(s(\tau),\tau) &= -2 \dot{s}(\tau).
\end{align} $$
Here $w(x,\tau)$ is the water temperature for a water-ice phase transition and $s(\tau) \le 0$ is the moving boundary, which starts at $s(0)=0$.
The associated optimal stopping problem, using van Moerbeke, is
$$ \begin{align}
u_{\tau} &= \frac{1}{2} u_{xx}, \quad x \in (s(\tau),\infty), \\
u(x,0) &= (k+1) x^2 \, 1_{\{x > 0 \}}, \\
u(s(\tau),\tau) &= \tau, \\
u_x(s(\tau),\tau) &= 0.
\end{align} $$
My main solver routine for the second problem is:
solverStefan[T_,k_,nexoppsperyear_,initsoln_,xmin_,xmax_,npts_]:=
Module[{xgrid,Soln,h,dt,hsoln,ecnt=0},
xgrid = xmin+(xmax-xmin)N[Table[i/npts,{i,0,npts}]];
dt = N[1/nexoppsperyear];
Soln =
h/.NDSolve[{D[h[x,t],t] == 0.5 D[h[x,t],{x,2}],
h[x,0] == initsoln[x],h[xmin,t] == t, h[xmax,t] == (k+1)(xmax^2+t),
WhenEvent[Mod[t,dt] == 0, ecnt++;
hsoln[x1_] := Max[h[x1,t], t];
h[x,t]->Outer[hsoln[#1]&,xgrid]]},{h},{x,xmin,xmax},{t,0,T}, (* MUST USE {t,0,T} *)
MaxSteps->1000000, MaxStepFraction->Min[dt/(10 T),1/npts],
Method->{"MethodOfLines",
"SpatialDiscretization"->{"TensorProductGrid","Coordinates"->xgrid}}][[1]];
Return[Soln]]
What is going on is that there is a reward for stopping early, namely
$\tau$. The WhenEvent method interrupts the solver repeatedly, and checks
to see at what spatial points the current pde solution falls below the reward for stopping. If the stopping reward is higher, it replaces the solution with that reward.
In finance language, the reward $\tau$ is the payoff to the option buyer on early exercise of the option. If the option is not exercised early, the option buyer receives $u(x,0)$, which is a quadratic on $x>0$.
I call the solver routine with
StefanBoundary[T_,k_,xmin_,xmax_,npts_,noppsperyear_,size_]:=
Module[{x1,initsoln,soln,g,MyTimeValue,eefunc,arg,alpha,s,
eeexact,p1,p2a,p2},
Off[NDSolve::eerri];
(* initial soln *)
initsoln[x1_]=If[x1>0, (k+1) x1^2,0];
soln = solverStefan[T,k,noppsperyear,initsoln,xmin,xmax,npts];
(* reward function *)
g[x1_,t1_]:= If[t1>0,t1,initsoln[x1]];
MyTimeValue[x1_,t1_] := soln[x1,t1]-g[x1,t1];
eefunc[x1_,t1_] := If[Chop[MyTimeValue[x1,t1]]>0,1,0];
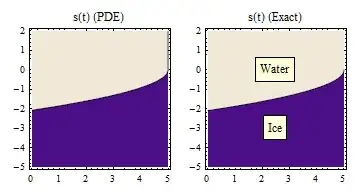
p1 = ContourPlot[eefunc[x1,T-t1],{t1,0,T},{x1,xmin,2},
Contours->2,ContourShading->True,PlotPoints->100,PlotLabel->"s(t) (PDE)",
ImageSize->size];
(* Exact boundary *)
arg[a_] := a CN[a]-k E^(-a^2/2)/Sqrt[2 Pi];
alpha = a/.FindRoot[arg[a],{a,1}];
s[t_] := -alpha Sqrt[t];
eeexact[x1_,t1_] := If[x1>s[t1],1,0];
p2a = ContourPlot[eeexact[x1,T-t1],{t1,0,T},{x1,xmin,2},
Contours->2,ContourShading->True,PlotPoints->100,
ImageSize->size,PlotLabel->"s(t) (Exact)"];
p2 = Show[p2a,Graphics[Inset[Framed[Style["Ice",12],
Background->LightYellow],{T/2,-3.0}]],
Graphics[ Inset[Framed[Style["Water",12],
Background->LightYellow],{T/2,0}]]];
Print["Stefan:finished: MMU=",MMU," GB"];
Return[GraphicsRow[{p1,p2},Spacings->0]]]
</pre>
Some auxiliary functions used are:
<pre>
MMU: = N[MaxMemoryUsed[]/10^9];
Cumnormal[xx_] := (1+Erf[xx/Sqrt[2]])/2;
CN = Cumnormal;
Running
StefanBoundary[5,3,-5,5,500,500,175]
yields the NDSolve boundary on the left and the exact on the right:



D[s[t]]should bes'[t]. (Of course this won't solve your problem… ) – xzczd Sep 01 '14 at 08:51