Removing elements from a list which appear in another list

Question

There are two lists {a, b, c, a, d, a, e} and {a, c, a}. I need to remove those elements from the first list which appears in a second list, to get {b, d, a, e}

Answer 1

New proposal

I was thinking about this problem today and came up with a new approach. In testing it appears to be competitively fast, often notably faster than any other method yet posted. It is also quite clean.

A limitation shared with rasher's uc: all elements in the drop list must be present in the main list.

fastRF[a_List, b_List] :=
  Module[{c, o, x},
    c = Join[b, a];
    o = Ordering[c];
    x = 1 - 2 UnitStep[-1 - Length[b] + o];
    x = FoldList[Max[#, 0] + #2 &, x];
    x[[o]] = x;
    Pick[c, x, -1]
  ]

The question example:

fastRF[{a, b, c, a, d, a, e} , {a, c, a}]

{b, d, a, e}

Timings

The prior frontrunners for performance are Leonid's unsortedComplement and rasher's uc. I shall compare these to fastRF as well as my earlier removeFrom2. Here is a chart showing the performance of each function at removing a variable number of elements (second parameter) from a starting list of one million elements (first parameter). Timings performed in version 10.0.2.

Needs["GeneralUtilities`"]

one = RandomInteger[1*^5, 1*^6];

BenchmarkPlot[
  {
   removeFrom2[one, #] &,
   unsortedComplement[one, #] &,
   uc[one, #] &,
   fastRF[one, #] &
  },
  RandomSample[one, #] &,
  5^Range[8],
  TimeConstraint -> 30
]

For all values (in this test) fastRF is indeed the fastest.

Explanation

The code above is quite opaque compared to my more direct and literal first answer. I think an explanation is in order.

The list of elements-to-remove, named b, is inserted at the beginning of main list, named a. Then the Ordering of this combined list is found. For the question example that looks like this, juxtaposed with the sorted list for illustration:

com = {a, c, a, a, b, c, a, d, a, e}
ord = Ordering[com]
com[[ord]]

{a, c, a, a, b, c, a, d, a, e}
{1, 3, 4, 7, 9, 5, 2, 6, 8, 10}
{a, a, a, a, a, b, c, c, d, e}

1, 2, 3 in ord are the elements to drop, each along with a copy from the main list. For example 4 and 7 should be dropped because of 1 and 3, and 6 should be dropped because of 2. To achieve this I first apply numeric transformations including UnitStep to turn the drop values to 1 and all others to -1. I then use FoldList for a modified accumulate process:

1 - 2 UnitStep[-1 - 3 + ord]
x = FoldList[Max[#, 0] + #2 &, %]

{1, 1, -1, -1, -1, -1, 1, -1, -1, -1}
{1, 2, 1, 0, -1, -1, 1, 0, -1, -1}

Each -1 in the output is an element to keep; all others are elements to drop. I then need to put this list back into the original order of the combined list (com). I use the method Simon Woods posted in Sort two lists at the same time, based on another due to its superior performance. All that remains is to Pick the elements of com that correspond to the -1's in x:

x[[ord]] = x; x

Pick[com, x, -1]

{1, 1, 2, 1, -1, 0, 0, -1, -1, -1}
{b, d, a, e}

Answer 2

Please see my second answer; the method therein is far more efficient than the ones below.

---

removeFrom[b_List, a_List] := Module[{f},
  f[_] = 0;
  (f[#] = -#2) & @@@ Tally[a];
  Pick[b, UnitStep[f[#]++ & /@ b], 1]
]

removeFrom[{a, b, c, a, d, a, e}, {a, c, a}]

{b, d, a, e}

---

Here somewhat longer but also a bit more efficient:

removeFrom2[b_List, a_List] := Module[{f, g},
  (f[#] = -#2) & @@@ Tally[a];
  g[x_] /; f[x] < 0 := f[x]++;
  g[_] = True;
  Select[b, g]
]

This avoids incrementing counters for elements that will never be dropped.

With some data this is not too far behind Leonid's method:

short = RandomInteger[1*^5, 2*^4];
long  = RandomInteger[1*^5, 2*^5];

unsortedComplement[long, short] // Short // Timing
removeFrom2[long, short]        // Short // Timing

{0.202, {68819,45303,67901,31724,23958,11781,29518,20287,46528,<<183297>>,75098,80755,34879,14667,67114,86027,24796,95072,59695}}

{0.25, {68819,45303,67901,31724,23958,11781,29518,20287,46528,<<183297>>,75098,80755,34879,14667,67114,86027,24796,95072,59695}}

Where there is heavy duplication Leonid's method is still much faster than mine.

Answer 3

Implementation

I am sure I missed a more elegant / short version, but here is an implementation which will be efficient even for large lists:

Clear[unsortedComplement];
unsortedComplement[x_, y_] :=
  Module[{order, xsorted, distinct, freqs, posintervals, freqrules},
    xsorted = x[[order = Ordering[x]]];
    {distinct, freqs} = Transpose[Tally[xsorted]];
    freqrules = Dispatch[Append[Rule @@@ Tally[y], _ -> 0]];
    posintervals =
      Transpose[{
         Most[#] + Replace[distinct, freqrules, {1}],
         Rest[#] - 1
      }] &[Prepend[Accumulate[freqs], 0] + 1];
    x[[Sort@order[[Flatten[Range @@@ posintervals]]]]]]

It borrows main ideas from here, but modifies it to the needs of the problem at hand. Once position intervals for elements in the sorted main list are found, they are shrinked by the number of same elements present in the second list, from the start (from the left end). From this, I generate partial list of positions in the ordered list, and reverse that via the ordering of that list, to get a list of positions in the original list. The algorithm has a log-linear complexity in the length of the first list and linear complexity in the length of the second list.

Examples and benchmarks

We have

unsortedComplement[{a,b,c,a,d,a,e},sub = {a,c,a}]
(* {b,d,a,e}  *)

for larger lists:

large1 = RandomInteger[1000,10^5];
large2 = RandomInteger[1000,10^4];
(res1=unsortedComplement[large1,large2])//Short//Timing
(* {0.078,{951,956,345,459,345,951,956,<<89986>>,443,977,568,340,496,887,946}} *)
(res2=Fold[Delete[#1,Position[#1,#2,1,1]]&,large1,large2])//Short//Timing
(* {35.,{951,956,345,459,345,951,956,<<89986>>,443,977,568,340,496,887,946}} *)
res1==res2
(* True *)

Answer 4

A much faster method. Based on my method for multiple-position finding:

uc[list_, eles_] := Module[{dt = Tally[eles], fm},
  fm = findMultiPosXX[list, dt[[All, 1]]];
  list[[Delete[Range@Length@list, 
               Transpose[{Flatten[MapThread[Take, {fm, dt[[All, 2]]}]]}]]]]]

Caveats: I assume the list of elements to be deleted is a subset of the target list. Easily modified if that's not the case.

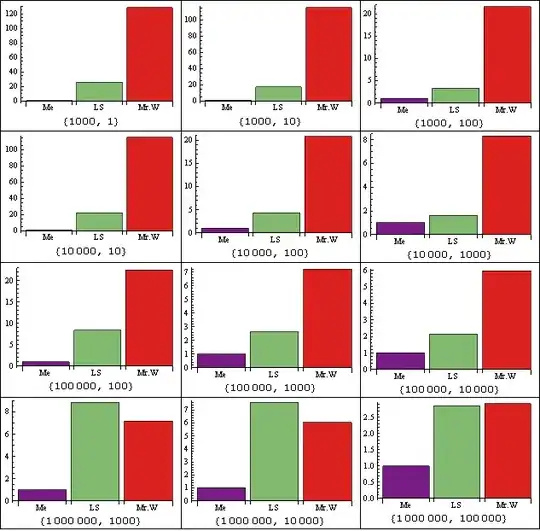
A quick performance comparison with the two fasted methods posted previously. Relative performance (time, normalized to 1 for the fastest), on a list generated with RandomInteger[size,1000000]. Labels correspond to size of "unique" pool of the 1000000 elements and number of elements deleted ( 1/10%, 1%, and 10% for each size). Over this test set, the average advantage is about 9X faster than the fastest alternative of each set, ranging from about a 65% advantage to over 12000% :

Answer 5

 list1 = {a, b, c, a, d, a, e}; list2 = {a, c, a};
 Fold[Delete[#1, Position[#1, #2, 1, 1]] &, list1, list2]
 (* {b, d, a, e} *)

or

 With[{patt = Table[Unique[], {Length[list2] + 1}]},
 ReplaceAll[list1,  Riffle[Pattern[#, BlankNullSequence[]] & /@ patt, list2] :> patt]]
 (*  {b, d, a, e} *)

Answer 6

Here's a slightly unconventional solution using patterns, and is very compact too:

{list1, list2} = {{a, c, a}, {a, b, c, a, d, a, e}};
Fold[# /. #2 &, list2, {h___, #, t___} :> {h, t} & /@ list1]
(* {b, d, a, e} *)

This exploits the fact that by default, BlankNullSequence[] seeks the Shortest sequence, thus you end up eating the occurrences from the left, as desired.

Answer 7

In Mathematica 9.0.0 there are several undocumented functions for dealing with hash maps explicitly.

• Language`HashMap[key1->val1, key2->val2, ...] creates new hash map from rules
• Language`HashMapAssociate[hmap, key, value] adds new key/value pair
• Language`HashMapLookup[hmap, key] returns value associated with a key

Here is the solution based on these functions:

remover[long_List, short_List] := Module[{hmap, lookupresult},
  hmap = Language`HashMap@@Apply[Rule, Tally[short], {1}];
  Select[long, (lookupresult = Language`HashMapLookup[hmap, #];
     Or[lookupresult === $Failed, lookupresult === 0, 
      (hmap = Language`HashMapAssociate[hmap, #, lookupresult - 1]; False)]) &]
  ]

But for this particular question solutions by Leonid and Mr.Wizard are faster.

Answer 8

Dirty and slow...

v1 = {a, b, c, a, d, a, e};
v2 = {a, c, a};

Flatten[Table @@@ Fold[Function[{list, ele}, 
    If[#1 === ele, {#1, If[#2 - 1 >= 0, #2 - 1, 0]}, {#1, #2}] & @@@ list], Tally[v1], v2]]

{a,b,d,e}

Answer 9

DeleteElements(since V 13.1) makes this rather complicated problem surprisingly simple:

list = {a, b, c, a, d, a, e};
remove = {a, c, a};

Remove up to 2 instances of a and up to 1 instance of c

rule = Rule @@ Reverse @ Transpose @ Tally @ remove

{2, 1} -> {a, c}

DeleteElements[list, rule]

{b, d, a, e}

Addendum

Like kglr proposed in his comment we can skip the definition of rule and simply write:

DeleteElements[list, 1 -> remove]

Answer 10

The positions of the elements to be deleted:

pos = Catenate@MapThread[Take[#1, #2] &, {Lookup[PositionIndex[list], Union@#], 
      Values[Counts[#]]}] &@remove;

Then, using Replacepart:

ReplacePart[list, Thread[pos -> Nothing]]
({b, d, a, e})

A variant of @eldo's solution using Counts is the following:

rule = Rule @@ {Values[#], Keys[#]} &@Counts[remove]
DeleteElements[list, rule]
({b, d, a, e})

Answer 11

An approach using Reap and Sow avoiding rescanning list.

Simple Approach where order does not matter

simple[h_, p_] := 
 Join @@ (Table[#[[1]], {#[[2]]}] & /@ 
    Cases[Last@
      Reap[Sow[1, #] & /@ h; Sow[-1, #] & /@ p, _, {#1, Total@#2} &], 
     Except[{_, 0}]])

For the test case this yields:

{a, b, d, e}

Perhaps, not the desired outcome.

Order matters

This is somewhat messy but I post anyway. Most of the code relates to order:

comp[x_, y_] := Module[{},
  fun[q_] := 
   If[Length[q] == 1, q, 
    Drop[#[[1]], Length[#[[2]]]] &@GatherBy[q, Sign]];
  ls[u_, v_] := 
   Cases[Last@
     Reap[Join[Table[Sow[j, u[[j]]], {j, Length[u]}], 
       Table[Sow[-j, v[[j]]], {j, Length[v]}]], _, {#1, fun[#2]} &], 
    Except[{_, {}}]];
  ord[u_] := Module[{pos, tab, or},
    pos = Flatten@u[[All, 2]];
    or = Thread[Sort[pos] -> Range[Length[pos]]];
    tab = Table[1, {Length[pos]}];
    ReplacePart[tab, 
     Flatten@(Thread[#[[2]] -> #[[1]]] & /@ (u /. or))]];
  ord[ls[x, y]]]

For the test case this yields the desired:

{b, d, a, e}