You can take advantage of the VertexNormals that Plot computes to translate the surface a little to each side. I'm not sure just what is required for good STL output. I put a polygonal side all around the two surfaces. The VertexNormals are wrong for the sides, so I commented them out for the image presented.
The thickness is controlled by the parameter thickness.
With[{plot = Plot3D[{(2*x*y)/(x^2 + y^2)}, {x, -2, 2}, {y, -2, 2}, Mesh -> None]},
With[{n0 = VertexNormals /. Cases[plot, HoldPattern[VertexNormals -> _], Infinity],
thickness = 0.1},
With[{pts = First @
Cases[plot,
GraphicsComplex[p_, e__] :> Flatten[{p - thickness n0, p + thickness n0}, 1],
Infinity],
vn = First @ Cases[plot, HoldPattern[VertexNormals -> v_] :> Join[v, v], Infinity]},
Graphics3D[
GraphicsComplex[
pts,
{EdgeForm[],
Cases[plot, Polygon[p_] :> Polygon@Join[p, p + Length[pts]/2], Infinity],
Cases[plot,
Line[p_] :> Polygon[Join[#, Reverse@# + Length[pts]/2] & /@ Partition[p, 2, 1]],
Infinity]}
(*, VertexNormals -> vn *)
],
PlotRange -> All,
Options[plot]
]
]]]
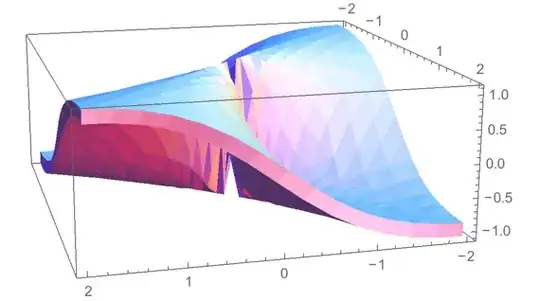
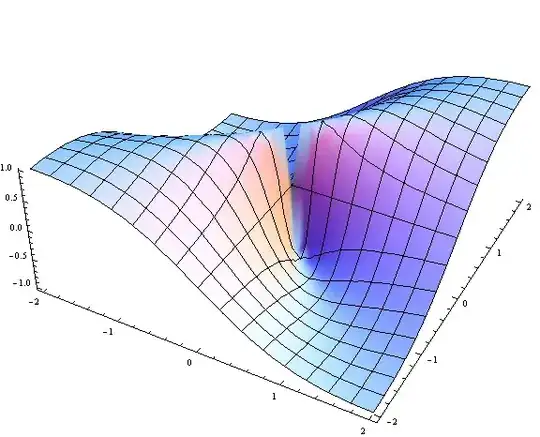



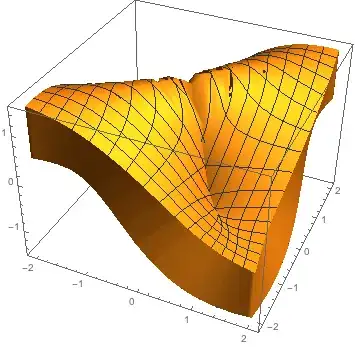
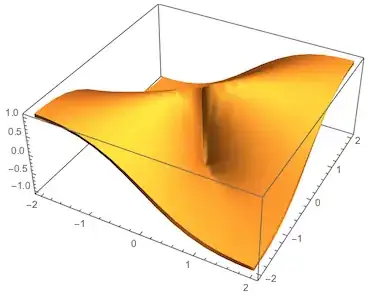
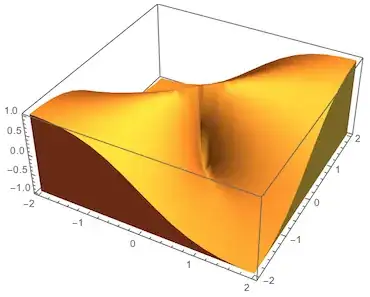
RegionPlot3D[]– Dr. belisarius Nov 24 '13 at 01:49