An efficient circular arc primitive for Graphics3D

Question

As many people have noted, the 2D graphics primitive Circle doesn't work in a Graphics3D environment (even in v10.0-v10.4, where many geometric regions were added). Several solutions to this problem have been proposed, both on this site and on StackOverflow.

They all have the disadvantage that they result in either rather ugly circles or highly inefficient ones because these circles were generated using polygons with several hundreds of edges, making interactive graphics incredibly slow. Other alternatives involve the use of ParametricPlot which doesn't generate efficient graphics either or yield a primitive that can't be used with GeometricTransformation.

I would like to have a more elegant solution that creates a smooth circular arc in 3D without requiring zillions of coordinates. The resulting arc should be usable in combination with Tube and can be used with GeometricTransformation.

Answer 1

In principle, Non-uniform rational B-splines (NURBS) can be used to represent conic sections. The difficulty is finding the correct set of control points and knot weights. The following function does this.

---

UPDATE (2016-05-22): Added a convenience function to draw a circle or circular arc in 3D specified by three points (see bottom of post)

EDIT : Better handling of cases where end angle < start angle

---

ClearAll[splineCircle];
splineCircle[m_List, r_, angles_List: {0, 2 π}] :=
 Module[{seg, ϕ, start, end, pts, w, k},
   {start, end} = Mod[angles // N, 2 π];
   If[ end <= start, end += 2 π];
   seg = Quotient[end - start // N, π/2];
   ϕ = Mod[end - start // N, π/2];
   If[seg == 4, seg = 3; ϕ = π/2];
   pts = r RotationMatrix[start ].# & /@ 
     Join[Take[{{1, 0}, {1, 1}, {0, 1}, {-1, 1}, {-1,0}, {-1, -1}, {0, -1}}, 2 seg + 1], 
      RotationMatrix[seg π/2 ].# & /@ {{1, Tan[ϕ/2]}, {Cos[ ϕ], Sin[ ϕ]}}];
   If[Length[m] == 2, 
    pts = m + # & /@ pts, 
    pts = m + # & /@ Transpose[Append[Transpose[pts], ConstantArray[0, Length[pts]]]]
   ];
   w = Join[
        Take[{1, 1/Sqrt[2], 1, 1/Sqrt[2], 1, 1/Sqrt[2], 1}, 2 seg + 1], 
        {Cos[ϕ/2 ], 1}
       ];
   k = Join[{0, 0, 0}, Riffle[#, #] &@Range[seg + 1], {seg + 1}];
   BSplineCurve[pts, SplineDegree -> 2, SplineKnots -> k, SplineWeights -> w]
 ] /; Length[m] == 2 || Length[m] == 3

This looks rather complex, and it is. However, the output (the only thing that ends up in the final graphics) is clean and simple:

splineCircle[{0, 0}, 1, {0, 3/2 π}]

Just a single BSplineCurve with a few control points.

It can be used both in 2D and 3D Graphics (the dimensionality of the center point location is used to select this):

DynamicModule[{sc},
 Manipulate[
  Graphics[
    {FaceForm[], EdgeForm[Black], 
     Rectangle[{-1, -1}, {1, 1}], Circle[], 
      {Thickness[0.02], Blue, 
       sc = splineCircle[m, r, {start Degree, end Degree}]
      }, 
      Green, Line[sc[[1]]], Red, PointSize[0.02], Point[sc[[1]]]
    }
  ],
  {{m, {0, 0}}, {-1, -1}, {1, 1}},
  {{r, 1}, 0.5, 2},
  {{start, 45}, 0, 360},
  {{end, 180}, 0, 360}
  ]
 ] 

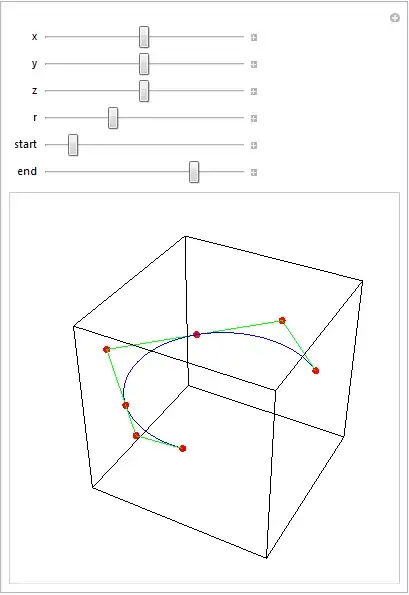
Manipulate[
 Graphics3D[{FaceForm[], EdgeForm[Black], 
   Cuboid[{-1, -1, -1}, {1, 1, 1}], Blue, 
   sc = splineCircle[{x, y, z}, r, {start Degree, end Degree}], Green,
    Line[sc[[1]]], Red, PointSize[0.02], Point[sc[[1]]]}, 
  Boxed -> False],
 {{x, 0}, -1, 1},
 {{y, 0}, -1, 1},
 {{z, 0}, -1, 1},
 {{r, 1}, 0.5, 2},
 {{start, 45}, 0, 360},
 {{end, 180}, 0, 360}
 ]

With Tube and various transformation functions:

Graphics3D[
  Table[
   {
    Hue@Random[],
    GeometricTransformation[
     Tube[splineCircle[{0, 0, 0}, RandomReal[{0.5, 4}], 
       RandomReal[{π/2, 2 π}, 2]], RandomReal[{0.2, 1}]], 
     TranslationTransform[RandomReal[{-10, 10}, 3]].RotationTransform[
       RandomReal[{0, 2 π}], {0, 0, 1}].RotationTransform[
       RandomReal[{0, 2 π}], {0, 1, 0}]]
    },
   {50}
   ], Boxed -> False
  ]

---

Additional uses

I used this code to make the partial disk with annular hole asked for in this question.

---

Specification of a circle or circular arc using three points

[The use of Circumsphere here was a tip by J.M.. Though it doesn't yield an arc, it can be used to obtain the parameters of an arc]

[UPDATE 2020-02-08: CircleThrough, introduced in v12, can be used instead of Circumsphere as well]

Options[circleFromPoints] = {arc -> False};

circleFromPoints[m : {q1_, q2_, q3_}, OptionsPattern[]] :=
Module[{c, r, ϕ1, ϕ2, p1, p2, p3, h, 
        rot = RotationMatrix[{{0, 0, 1}, Cross[#1 - #2, #3 - #2]}] &},
  {p1, p2, p3} = {q1, q2, q3}.rot[q1, q2, q3];
  h = p1[[3]];
  {p1, p2, p3} = {p1, p2, p3}[[All, ;; 2]];
  {c, r} = List @@ Circumsphere[{p1, p2, p3}];
  ϕ1 = ArcTan @@ (p3 - c);
  ϕ2 = ArcTan @@ (p1 - c);
  c = Append[c, h];
  If[OptionValue[arc] // TrueQ,
    MapAt[Function[{p}, rot[q1, q2, q3].p] /@ # &, splineCircle[c, r, {ϕ1, ϕ2}], {1}],
    MapAt[Function[{p}, rot[q1, q2, q3].p] /@ # &, splineCircle[c, r], {1}]
  ]
] /; MatrixQ[m, NumericQ] && Dimensions[m] == {3, 3}

Example of usage:

{q1, q2, q3} = RandomReal[{-10, 10}, {3, 3}];
Graphics3D[
 {
  Red,
  PointSize[0.02],
  Point[{q1, q2, q3}],
  Black,
  Text["1", q1, {0, -1}],
  Text["2", q2, {0, -1}],
  Text["3", q3, {0, -1}],
  Green,
  Tube@circleFromPoints[{q1, q2, q3}, arc -> True
  }
 ]

Similarly, one can define a 2D version:

 circleFromPoints[m : {q1_List, q2_List, q3_List}, OptionsPattern[]] :=
 Module[{c, r, ϕ1, ϕ2, ϕ3},
   {c, r} = List @@ Circumsphere[{q1, q2, q3}];
   If[OptionValue[arc] // TrueQ,
    ϕ1 = ArcTan @@ (q1 - c);
    ϕ2 = ArcTan @@ (q2 - c);
    ϕ3 = ArcTan @@ (q3 - c);
    {ϕ1, ϕ3} = Sort[{ϕ1, ϕ3}];
    splineCircle[c, r, 
     If[ϕ1 <= ϕ2 <= ϕ3, {ϕ1, ϕ3}, {ϕ3, ϕ1 + 2 π}]],
    splineCircle[c, r]
    ]
   ] /; MatrixQ[m, NumericQ] && Dimensions[m] == {3, 2}

Demo:

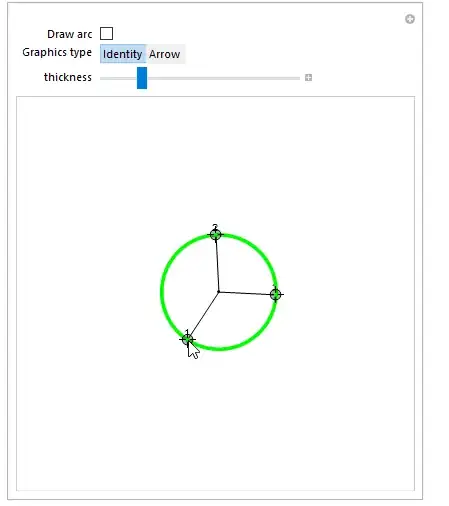
Manipulate[
 c = Circumsphere[{q1, q2, q3}][[1]];
 Graphics[
  {
   Black,
   Line[{{q1, c}, {q2, c}, {q3, c}}],
   Point[c],
   Text["1", q1, {0, -1}],
   Text["2", q2, {0, -1}],
   Text["3", q3, {0, -1}],
   Green,
   Thickness[thickness], Arrowheads[10 thickness],
   sp@circleFromPoints[{q1, q2, q3}, arc -> a]
   }, PlotRange -> {{-3, 3}, {-3, 3}}
  ],
 {{q1, {0, 0}}, Locator},
 {{q2, {0, 1}}, Locator},
 {{q3, {1, 0}}, Locator},
 {{a, False, "Draw arc"}, {False, True}},
 {{sp, Identity, "Graphics type"}, {Identity, Arrow}},
 {{thickness, 0.01}, 0, 0.05}
 ]

For versions without Circumsphere (i.e, before v10.0) one could use the following function to get the circle center (c in the code above, r would then be the EuclideanDistance between c and p1):

getCenter[{{p1x_, p1y_}, {p2x_, p2y_}, {p3x_, p3y_}}] := 
   {(1/2)*(p1x + p2x + ((-p1y + p2y)*
           ((p1x - p3x)*(p2x - p3x) + (p1y - p3y)*(p2y - p3y)))/
            (p1y*(p2x - p3x) + p2y*p3x - p2x*p3y + p1x*(-p2y + p3y))), 
    (1/2)*(p1y + p2y + ((p1x - p2x)*
            ((p1x - p3x)*(p2x - p3x) + (p1y - p3y)*(p2y - p3y)))/
            (p1y*(p2x - p3x) + p2y*p3x - p2x*p3y + p1x*(-p2y + p3y)))}

Answer 2

Might as well... what follows is a routine that isn't as general as the routine Sjoerd gave, but gives simpler results in some cases. This is based on work by Piegl and Tiller (see their nice book on NURBS as well).

arc[center_?VectorQ, {start_?VectorQ, end_?VectorQ}] := Module[{ang, co, r},
  ang = VectorAngle[start - center, end - center];
  co = Cos[ang/2]; r = EuclideanDistance[center, start];
  BSplineCurve[{start, center + r/co Normalize[(start + end)/2 - center], end}, 
   SplineDegree -> 2, SplineKnots -> {0, 0, 0, 1, 1, 1},
   SplineWeights -> {1, co, 1}]]

For example:

{Graphics[arc[{0, 0}, {{1, 1}, {-1, 1}}]],
 Graphics3D[arc[{0, 0, 0}, {{1, 1, 1}, {-1, 1, 1}}]]} // GraphicsRow

This routine works as long as the angle determined by the arc lies in the open interval $(0,\pi)$ (an inherent limitation of the simple method), and that EuclideanDistance[center, start] == EuclideanDistance[center, end] (otherwise, it draws an elliptical arc). For reflex angles (that is, angles in the interval $(\pi,2\pi)$), you will have to stitch together two of these arc[]s properly.

(A little note: though Piegl and Tiller show in their work that one can use negative weights to generate an arc corresponding to a reflex angle, BSplineCurve[] handles negative weights poorly by default:

Graphics[BSplineCurve[{{-1/Sqrt[2], 1/Sqrt[2]}, {0, Sqrt[2]}, {1/Sqrt[2], 1/Sqrt[2]}},
                      SplineDegree -> 2, SplineKnots -> {0, 0, 0, 1, 1, 1},
                      SplineWeights -> {1, -1/Sqrt[2], 1}], 
         PlotRange -> {{-1, 1}, {-1, 1}}]

but one can use an undocumented option setting to improve the rendering:

Graphics[BSplineCurve[{{-1/Sqrt[2], 1/Sqrt[2]}, {0, Sqrt[2]}, {1/Sqrt[2], 1/Sqrt[2]}},
                      SplineDegree -> 2, SplineKnots -> {0, 0, 0, 1, 1, 1},
                      SplineWeights -> {1, -1/Sqrt[2], 1}],
         BaseStyle -> {BSplineCurveBoxOptions -> {Method -> {"SplinePoints" -> 30}}}, 
         PlotRange -> {{-1, 1}, {-1, 1}}]

(with thanks to Mr. Wizard))

One can also use BSplineFunction[] in ParametricPlot[]:

f = BSplineFunction[{{-1/Sqrt[2], 1/Sqrt[2]}, {0, Sqrt[2]}, {1/Sqrt[2], 1/Sqrt[2]}}, 
                    SplineDegree -> 2, SplineKnots -> {0, 0, 0, 1, 1, 1}, 
                    SplineWeights -> {1, -1/Sqrt[2], 1}];
ParametricPlot[f[x], {x, 0, 1}]

Finally, here's how to render a unit semicircle with BSplineCurve[] (the generalization to the three-dimensional case is left to the reader):

Graphics[BSplineCurve[{{1, 0}, {1, 1}, {-1, 1}, {-1, 0}}, 
  SplineDegree -> 2, SplineKnots -> {0, 0, 0, 1/2, 1, 1, 1}, 
  SplineWeights -> {1, 1/2, 1/2, 1}]]

Again, see Piegl and Tiller's work if you want to learn more about these things.

Answer 3

This is more an extended comment than an answer. Sjoerd C. de Vries' answer is already almost perfect. However, as @J.M. already pointed out, a bit of linear algebra may improve efficiency.

1. Some time ago, I found out for myself that RotationMatrix is pretty slow compared to straightforwardly setting up the matrix by hand.

2. For a matrix A, we have that A multiplied from the left to a vector is the same as Transpose[A] multiplied from the right, so that we can replace A.# & /@ x with the more efficient x.Transpose[A].

3. Moreover, m + # & /@ can be vectorized by ConstantArray[m, Length[x]] + x.

With these small modifications and some other minor tweeks (that do not improve the readability, though), the new code looks as follows:

ClearAll[splineCircle2];
splineCircle2[m_List, r_, angles_List: {0., 2. π}] := 
 Module[{seg, ϕ, start, end, pts, w, k, pihalf},
   pihalf = 0.5 π;
   {start, end} = Mod[N[angles], 2. π];
   If[end <= start, end += 2. π];
   seg = Quotient[N[end - start], pihalf];
   ϕ = Mod[N[end - start], pihalf];
   If[seg == 4, seg = 3; ϕ = pihalf];
   With[{
     cseg = Cos[pihalf seg], sseg = Sin[pihalf seg],
     cϕ = Cos[ϕ], sϕ = Sin[ϕ], 
     tϕ = Tan[0.5 ϕ],
     rcs = r Cos[start], rss = r Sin[start]
     },
    pts = Join[
       Take[{{1., 0.}, {1., 1.}, {0., 1.}, {-1., 1.}, {-1., 0.}, {-1., -1.}, {0., -1.}}, 2 seg + 1],
       {{cseg - sseg tϕ, sseg + cseg tϕ}, {cseg cϕ - sseg sϕ, cϕ sseg + cseg sϕ}}
       ].{{rcs, rss}, {-rss, rcs}}
    ];
   pts = ConstantArray[m, Length[pts]] + 
     If[Length[m] == 2, 
      pts, 
      Join[pts, ConstantArray[{0.}, Length[pts]], 2]
     ];
   w = With[{c = 1./Sqrt[2.]}, 
     Join[Take[{1., c, 1., c, 1., c, 1.}, 2 seg + 1], {Cos[0.5 ϕ], 1.}]
     ];
   k = Join[{0, 0, 0}, Riffle[#, #] &@Range[seg + 1], {seg + 1}];
   BSplineCurve[pts, SplineDegree -> 2, SplineKnots -> k, SplineWeights -> w]
   ] /; Length[m] == 2 || Length[m] == 3

The following test shows that this leads to a 7-fold speedup on my machine:

n = 2000;
mdata = RandomReal[{-1, 1}, {n, 2}];
rdata = RandomReal[{1, 2}, {n}];
a1data = RandomReal[{0., 2 π}, {n}];
a2data = a1data + RandomReal[{0., 2 π}, {n}];
data = Transpose[{mdata, rdata, Transpose[{a1data, a2data}]}];

aa = splineCircle @@@ data; // RepeatedTiming
bb = splineCircle2 @@@ data; // RepeatedTiming
Max[Abs[aa[[All, 1]] - bb[[All, 1]]]]
Max[Abs[aa[[All, 2]] - bb[[All, 2]]]]
Max[Abs[aa[[All, 3]] - bb[[All, 3]]]]

{0.78, Null}

{0.11, Null}

8.88178*10^-16

0

0

Answer 4

There are already some good answers here, but I will focus on brevity and simplicity in my two suggestions ... :

Suggestion 1 ... :

As already noted, use a BSplineCurve[...]. My only contribution to this part is brevity, and I basically took the code from the reference documentation... :

By using weights, you can make a rational B-spline, such as a circle

The code for this method is below ... :

Graphics3D@
 BSplineCurve[
  {{1/2, 0, 0}, {1, 0, 0}, {1, 1, 0}, {1/2, 1, 0}, {0, 1, 0}, {0, 0, 
    0}, {1/2, 0, 0}},
  SplineDegree -> 2,
  SplineKnots -> {0, 0, 0, 1/4, 1/2, 1/2, 3/4, 1, 1, 1}, 
  SplineWeights -> {1, 1/2, 1/2, 1, 1/2, 1/2, 1}
  ]

Suggestion 2 ... :

Intersect a Sphere[...] (the hollow version of a Ball[...] in Mathematica-parlance) with a plane. I prefer using Hyperplane[...] simply for convenience / brevity. Use RegionIntersection[...] to accomplish this suggestion...

The code for this method is below ... :

Region@RegionIntersection@{Hyperplane@{1, 0, 0}, 
    Sphere[]} // MacM1OpacityFix

This can be combined with other Graphics3D[...] objects using Show[...] (you cannot just include the region in the Graphics3D[...] directly, but the end-result is the same. I prefer this method.

[Non-] Suggestion 3 ... :

Finally, note that you CAN make a circle via an ImplicitRegion[...], but if anybody else tries to then use this in Graphics3D[...] like I did, I'll save you some time... The following successfully generates a circle, but the resulting output cannot be used in a Graphics3D[...]:

Region@ImplicitRegion[
  {x^2 + y^2 == 1},
  {x, y}
  ]

Update: This works, though ... :

Region@ImplicitRegion[
  {x^2 + y^2 <= 1, z == 1},
  {x, y, z}
  ]

or

Region@ImplicitRegion[{x^2 + y^2 == 1, z == 1}, {x, y, 
    z}] // MacM1OpacityFix

NOTE - Mac M1 Bug ... :

Note also that for whatever reason, a Mac M1 graphics-related issue prevents some of the above code from running on my machine without the fix referenced here ... : https://mathematica.stackexchange.com/a/255291

Namely ... :

MacM1OpacityFix = 
  Style[#, RenderingOptions -> {"3DRenderingEngine" -> "OpenGL"}] &;